Священная математика

Фукагава Хидэтоси, Тони Ротман

Издательство Принстонского университета
Принстон и Оксфорд

2008

eng->rus: shogi.ru, Д.К., 2011-2012
версия: 10.8.16 (30% готовности, без чертежей)

Содержание

• Обложка
• Предисловие Фримэна Дайсона
• Предисловие Фукагавы Хидэтоси
• Предисловие Тони Ротмана
• Благодарности
• Что мне следует знать, чтобы читать эту книгу?
• Обозначения


• 1. Япония и храмовая геометрия
• 2. Китайские корни японской математики
• 3. Японская математика и математики эпохи Эдо
• 4. Лёгкие задачи храмовой геометрии
• 5. Сложные задачи храмовой геометрии
• 6. Ещё более сложные задачи храмовой геометрии
• 7. Путевой дневник математика Ямагути Кандзана
• 8. Восток и Запад
• 9. Таинственное Энри
• 10. Введение в инверсию


• Примечания
• Для дальнейшего чтения
• Японские термины
• Имена собственные

Вслед за требованием, для решения задач сангаку необходимо большое число особых инструментов. У нас не было цели сделать из Священной Математики учебник, поэтому по большей части мы не учим основным методам. Если Вы пытаетесь решить эти задачи, хорошей идеей было бы иметь под рукой какой-нибудь стандартный учебник по геометрии для справки. Небольшое количество предложений, варьирующихся от элементарных до продвинутых, предложены в разделе Для дальнейшего чтения; тем не менее, даваемые нами вспомогательные намёки помогут Вам чуть точнее понять, что Вам понадобится.

Неизбежно нужен хороший чертёж. Многие из этих задач весьма тонки, и для них недостаточно сделать грубый набросок, который введёт Вас в заблуждение: Вам надо сделать аккуратный чертёж, отражающий подлинные условия задачи. Зачастую путь к решению будет очевиден, когда Вы нарисуете подходящие вспомогательные прямые.

Единственным наиболее важным математическим инструментом будет теорема Пифагора. Эта основная теорема, ставшая известной японцам из Китая, используется постоянно и повсюду, и для решения большой части задач достаточно её одной. Если же Вы не в ладах и с теоремой Пифагора, то задачи этой книги будут для Вас крайне сложны.

Если же вооружиться теоремой Пифагора, то многие, если не большинство, из данных задач потребуют решения квадратных уравнений. Вам часто будет нужна формула их решений, которая тоже была известна японцам, но зачастую окажется более удобным решать эти уравнения методом "составления полного квадрата". Практически столь же часто будете Вам встречаться и квадратные корни, обычно - из радиуса окружности, и поэтому Вам понадобится узнать такие основные методы обращения с квадратными корнями, как [rationalizing denominators].

Наиболее часто требующимся инструментом, после теоремы Пифагора и квадратных уравнений, являются, наверное, свойства подобных треугольников и теоремы про треугольники, у которых равны все соответствующие углы или угол и две стороны. Все они Вам понадобятся. Также, потребуются практически все тригонометрические тождества, включающие синусы, косинусы и тангенсы, то есть не только тождество sin²x + cos²x = 1, но и все его варианты, а также формулы половинных и двойных углов.

Всплывает часто и закон косинусов. Это обобщение теоремы Пифагора для неправильных треугольников, позволяющее вычислить сторону треугольника c по двум другим: c² = a² + b² - 2ab cos(x), где x - угол между a и b. Также, иногда появляется и закон синусов: a/sin(A) = b/sin(B) = c/sin(C), где A, B и C - углы треугольника, а a, b и c - противостоящие им стороны. Хотя традиционные японские математики и использовали тригонометрические функции лишь неявно, они пользовались их эквивалентами, и все эти соотношения были им понятны. Решения задач из глав 4 и 5 дадут более ясное видение того, как эти математики действовали.

Эти задачи решаются чаще рассмотрением площадей, чем длин сторон. Вместе с теоремой Пифагора, в них часто используется тот факт, что длины двух касательных, проведённых к окружности из одной внешней точки, равны. Этот факт иногда называют "теоремой об отрезках касательных". Если Вы не встречали его доказательство в начальном курсе, то можете попробовать доказать его сами; это очень легко. Также, часто встречается "теорема о пересекающихся хордах": если в окружности пересекаются две хорды, то произведение длин отрезков одной хорды, на которые её делит точка пересечения, равно произведению длин отрезков другой (см.рис.). Оставшиеся теоремы мы будем представлять по мере необходимости.

Для решения некоторых более сложных задач необходим "современный" приём, оказывающийся крайне полезным: это инверсия. Но поскольку инверсии больше не учат в школах (в США), мы включили главу (10), объясняющую этот мощный метод.

Горстка задач требует вычислений, но помимо лишь небольшого их числа это не заходит далее простейшего дифференцирования и интегрирования.

Обозначения

Мы попытались сделать обозначения, использующиеся во всей этой книге, стандартными и простыми, но из-за риска побеспокоить профессионалов попытались также избежать некоторых терминов, которые нечасто встречаются неамериканцами - таких, как "описанная окружность" и "перпендикуляр к основанию". (Очевидно, что крестьяне феодальной Японии такой терминологией не пользовались.) Когда избегание специальных терминов оказывается ненужным, и если мы не определяем их явно, то верим, что они будут определены по контексту. Например, "описанная окружность" - это просто окружность, в которую рассматриваемый многоугольник вписан, а "вписанная окружность" - это окружность, вокруг которой он описан. "Описанный центр" и "вписанный центр" - это центры соответствующих окружностей. Когда большое количество фигур расположено внутри, например, окружности так, что они они касаются друг друга, мы иногда говорим обо всём этом наборе, как "вписанном", хотя технически это и неправильное употребление термина.

В треугольниках вершины обозначаются заглавными буквами, а стороны - строчными. Сторона, противостоящая углу A, обычно называется a. Иногда мы используем символ угла, чтобы обозначить сам угол: ∠A. Все эти обозначения стандартны.

Большинство американских текстов использует для обозначения радиуса окружности радиальные линии или стрелки, но в японских задачах обычно фигурирует большое число окружностей, и нанесение на них большого числа радиальных линий затрудняет восприятие чертежей. Поэтому мы часто обозначаем радиус окружности просто точкой в её центре с надписанным рядом обозначением радиуса, r. Такой способ требует небольшого привыкания, но он оказался очень удобным. Важно также отметить, что часто мы говорим об окружности упоминанием её радиуса, т.е. "окружность r" означает окружность радиуса r.

Священная математика

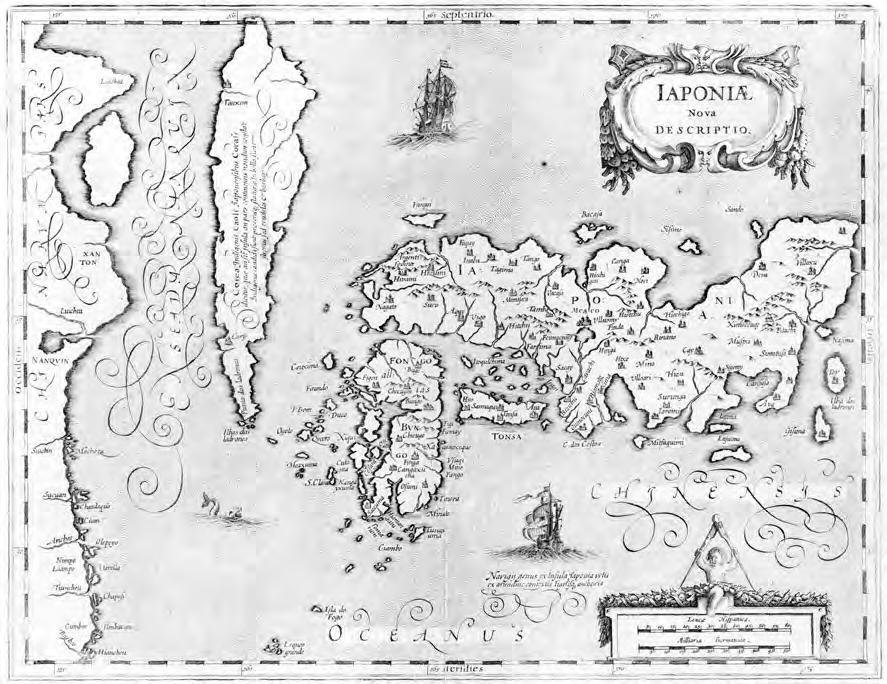
Рис. 1.1. Эта редкая карта Японии "Iaponi nova description" (Амстердам, 1647-1656) была составлена голландским картографом Яном Янссоном (1588-1664) и изготовлена на медном листе формата 33x43 см.

Глава 1. Япония и храмовая геометрия

Утихли колокольцы храма.
Остался аромат цветов.
Великолепный вечер!
Мацуо Басё

Храмы

Гостю иной страны не избежать опыта очарования и беспокойства, сопутствующих встрече с неизвестными традициями и обычаями. Некоторые гости пытаются превозмочь свои страхи, но большинство обычно отступает к привычным подпоркам, и тут пролегает различие: те, кто заключает культурный шок в объятия - путешественники; те, кто его не принимает - туристы.

Наиболее глубокий культурный шок возникает при столкновении с другим методом мышления. Большинство из нас едва ли может представить прогулку в Западную церковь или собор для встречи с цветными витражами, покрытыми уравнениями и геометрическими фигурами. Даже если мы себе это и представим, эта мысль ударит нас, как чужака, находящегося не на своём месте, возможно - святотатца. Однако в течение более двух веков японские математики - профессионалы, любители, женщины, дети - создавали то, что по сути было такими покрытыми математикой витражами: деревянные таблички, украшенные прекрасными геометрическими задачами, являвшиеся одновременно и произведениями искусства, и религиозными дарами, и записями того, что можно назвать "народной математикой". Создатели этих сангаку (дословно - "математическая табличка") вывешивали их тысячами в буддистских храмах и синтоистских святилищах по всей Японии, и по этой причине всё собрание задач сангаку стало известно, как "храмовая геометрия", священная математика.

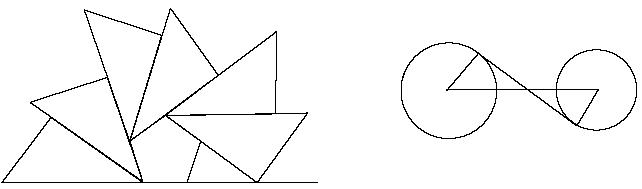
	Диаг. 1.1. Как Вы думаете, какой из этих чертежей взят из американского теста по геометрии?

Данная книга предлагает Вам не только встретиться с храмовой геометрией, но и оценить её. Для этого надо преодолеть небольшой культурный шок. Первого взгляда на сангаку достаточно, чтобы понять, что они создавались исходя из глубоко иной эстетики, чем вдохновлённые греками чертежи, которые можно найти в западных книгах по геометрии. На более глубоком уровне становится ясно, что методы, которые японские геометры применяли для решения таких задач, отличались, иногда весьма значительно, от своих западных аналогов. Спросите любого профессора математики, будут ли математические законы такими же в другой Вселенной, и он (или она) ответит: конечно, да. Настоящие математики - пифагорейцы: они не могут сомневаться, что математика существует независимо от человеческого ума. Вместе с тем, в свободное время математики часто рассуждают о том, сколь сильно взгляд на математику может отличаться от того, как её преподают в западных школах.

Храмовая геометрия даёт частичный ответ на оба этих вопроса. Да, законы математики на Западе и Востоке одни и те же, но также верно и то, что традиционные японские геометры, создававшие сангаку, видели свой математический мир другими глазами, и зачастую решали задачи методами, отличающимися от западных. Учиться традиционной японской математике - это учиться другому методу мышления.

	Рис.1.2. Анонимное и недатированное изображение на дереве (вероятно, середина XIX в.): гавань г. Нагасаки с островком Дэсима (в форме веера) на переднем плане. Вид на Дэсиму изображён, также, на рис.2. (© Музей Истории и Культуры г.Нагасаки)

Традиционная японская математика, а вместе с нею и храмовая геометрия, возникли в XVII веке при довольно уникальном наборе обстоятельств. В 1603 году, после победы над своими соперниками-феодалами (даймё) в битве при Сэкигахара, Токугава Иэясу стал сёгуном (военным правителем) Японии, установив сёгунат Токугава. Клан Токугава правил Японией почти 3 века, до 1868 года, когда через десятилетие после насильственного открытия Японии Западу Коммодором Мэттью Пэрри сёгунат рухнул.

Одним из первых шагов Иэясу после Сэкигахары стал перенос его штаба в маленький город-крепость в центральной Японии, который тогда назывался Эдо - нынешний Токио. Поэтому правление клана Токугава известно под названием эпоха Эдо. В первые годы сёгуната Токугава, Иэясу (проживший до 1616 г., но официально оставивший пост сёгуна в 1605-м) консолидировал власть, конфисковав земли других феодалов, однако во многом продолжил внешнюю политику своего предшественника, великого даймё Тоётоми Хидэёси. В начале XVII века Япония вела существенную торговлю с другими странами, как восточными, так и западными. Город Нагасаки на острове Кю:сю: стал базой, через которую "южные варвары" импортировали свои товары, а также печатные переводы западной литературы, во многом - религиозной.

Западные миссионеры присутствовали к тому моменту в Японии более 50 лет. Осенью 1543 года три португальца потерпели кораблекрушение около острова Кюсю. Это несчастье оказалось решающим для отношений Японии с внешними странами, поскольку эти люди имели аркебузы, которые были быстро приняты на вооружение японскими феодалами. Такое же, или даже большее значение имело то, что через небольшое число лет после этого судьбоносного кораблекрушения начали прибывать португальские купцы и иезуитские миссионеры, ища торговли и прозелитов. Особенно были успешны иезуиты, обратившие за следующие 40 лет 200.000 японцев, и ставшие по сути правителями региона Нагасаки.

Всё это обеспокоило сторонников буддизма и развило недоверие самого Хидэёси: в 1587 году он взял Нагасаки под свой прямой контроль и издал два эдикта, направленных на обуздание распространения христианства. Но вскоре прибыли испанцы, и испанские купцы стали соперничать с португальскими за торговлю, а францисканцы стали соперничать с иезуитами за прозелитизм. В 1596 году, после того, как испанцы предположительно проболтались, что эти миссионеры - лишь авангард иберийского завоевания, Хидэёси приказал казнить 26 священников и обращённых. Однако на уме у феодалов было другое, в частности - завоевание Китая, и он не смог достичь разрешения растущего напряжения между Японией и Западом.

Это напряжение разрешилось весьма решительным и грубым образом в самом конце жизни Токугавы Иэясу и в два следующих десятилетия. В 1614 году Токугава переиздал предыдущий эдикт, в котором он в целом приказывал, чтобы все христианские миссионеры покинули страну, чтобы места богослужений были ликвидированы, а практика христианства объявлена вне закона. Но вмешались другие внутренние обстоятельства, и Иэясу умер в 1616 году, не предприняв особых действий. Однако после его смерти началось ревностное преследование обращённых в христианство, и к 1637 году, по некоторым оценкам, 300.000 обращённых были признаны изменниками или убиты. Наконец, в 1639 году внук Иэясу, Токугава Иэмицу, издал серию декретов, предлагавших награду за выявление кириситан и запрещавших под страхом смерти японским кораблям уходить за моря, а японцам - путешествовать за границу.

В 1614 году последние португальские купцы были изгнаны, и остались лишь голландцы. Голландцы прибыли в Японию относительно поздно, в 1609 году, и проявили к торговле гораздо больше интереса, чем к миссионерству. Поэтому, после изгнания иберийцев, им было разрешено остаться. Однако теперь японцы, имевшие сильное подозрение к Западу, наложили на присутствие голландцев жёсткие ограничения: представители голландской Ост-Индской Компании были вынуждены переместиться на небольшой рукотворный остров под названием Дэсима в гавани Нагасаки (см. рис. 2 и 1.2). Этот остров в форме веера, изначально созданный для португальцев, имел размеры лишь 200×70 метров.Его окружала стена, увешанная надписями, запрещавшими японцам посещение, и он был полностью отрезан от большой земли, исключая бамбуковый водопровод и единственный охраняемый мост. На этом оазисе, в ожидании прихода голландских кораблей, жило около 20 представителей Ост-Индской Компании, с небольшим числом складов, овец, свиней и куриц. Прибывая в порт, капитаны закрывали все Библии и христианские книги в бочке, пока японские рабочие перетаскивали грузы.

	Рис. 1.3 - карта административного деления Японии.

Два следующих века это составляло всю торговлю Японии с Западом, и таким образом началась политика сакоку - "закрытой страны". Невозможно утверждать, что сакоку была на 100% эффективна; определённо, продолжалась торговля с Кореей и Китаем. Около 1650-го года два японца убежали в Голландию, чтобы изучать математику. Этих учёных мы знаем лишь по их принятым именам: Петриус Хартсингиус и Францискус Каррон, дающим хоть какое-то различение. Мы не знаем, вернулись ли они в Японию. Один доктор, Накасима Тё:дзабуро:, путешествовал с голландским торговцем и рискнул возвратиться домой. Исполняя традицию, местный даймё лишил Накасиму жизни, хотя тот и вылечил одного из больных голубей этого феодала.

Такая информационная отрезанность заставляет верить, что по обычным стандартам изоляция от Запада была практически полной. Касательно математики, было весьма маловероятно, чтобы кто-то в Японии узнал о создании современных методов высчислений Ньютоном и Лейбницем в конце XVII века, и явно, судя по задачам сангаку и традиционным математическим японским текстам, нет свидетельств того, чтобы их авторы понимали фундаментальные теоремы методов высчислений.

Из такого положения дел вовсе не следует делать вывод, что сакоку имело полностью негативные последствия. Напротив, эта политика была столь успешна в устранении международных конфликтов, что 250 лет эпохи Эдо стали известны, как "Великое Перемирие". Более того, при стабильности, обеспеченной сёгунатом Токугава, японская культура испытывала блестящее цветение, так что годы конца XVII века известны под названием Гэнроку - "Ренессанс". В то время самураи культивировали искусность в "медицине, поэзии, чайной церемонии, музыке, барабанном бое, танце но, этикете, должны были разбираться в судостроении, арифметике, вычислениях... не говоря о литературной композиции, чтении и письме. Было много и других тем..." 1.

У нас нет тут места, чтобы подробно распространяться о богатствах культуры Гэнроку, но следует понимать, что в эту эпоху многие из искусств, которыми Япония была известна, достигли наивысшего расцвета: расцвёл танец Но, великий драматург Чикамацу Мондзаэмон (1653-1725) писал пьесы для театра Кабуки и кукольных театров; на подъёме были чайная церемония, цветочная композиция и садовая архитектура, а также художество нескольких школ, включая вездесущие укиё-э, или оттиски "плывущего мира", просвещавшие полусвет куртизанок и эротической любви, и явно определившие всю эпоху. Оттиски укиё-э делались на деревянных основах не потому, что в Японии не хватало лёгких носителей, которые во времена Хидэёси импортировались из Кореи, но потому, что художники предпочитали возможности каллиграфии и искусства, предоставляемые печатью на дереве. Не была в затмении и поэзия, особенно хайку, достигшие некоторых из своих величайших выражений в работах Мацуо Басё: (1644-1694), которые ещё долгое время признавались во всём мире.

	Рис. 1.4. Это укиё-э из серии "36 видов горы Фудзи" Кацусика Хокусая (1760-1849), одного из известнейших художников эпохи Эдо. На картине изображён вид Эдо из храма Ракан-дзи в Хондзё. Оригинал - цветной. (© Nagoya TV-Japan)

Что удивляюще отсутствует в стандартных обзорах японских культурных достижений этого периода, так это любое упомининие математических наук. Хотя изоляция и произвела столь особую эстетизацию в искусствах, определённо, не меньшее влияние оказала она и в этих сферах. Стилистическая форма её влияния на геометрию станет последовательно видна читателям, которые погрузятся в математические аспекты данной книги; многие задачи сангаку не случайно напоминают образцы оригами, и неслучайно практика вывешивания табличек началась именно во время Гэнроку, ибо, как мы вскоре увидим, именно во второй половине XVII века традиционная японская математика и начала цвести.

Независимо от формального развития математики того времени, западные читатели неизменно хотят узнать, как возник этот странный обычай вывешивать таблички в святилищах и храмах. Но в контексте Японии это было весьма естественно. Японская национальная религия, синтоизм, населена "восьми миллионами духов", или ками ^1', наполняющих собою всё, от солнца и луны до рек, гор и деревьев. За столетия до появления сангаку почитатели синто уже приносили дары в местные святилища. Считалось, что ками любят лошадей, но лошади были дороги, и почитатели, которые не могли предложить живую, могли подарить вместо этого её изображение на дереве. Действительно, на многих табличках XV века и ранее изображены лошади.

Таким образом, для японцев не было ничего особо странного в вывешивании математической таблички в храме. Мы не можем сказать точно, в каком году или десятилетии эта традиция зародилась, но старейшая из сохранившихся сангаку, найденная в префектуре Точиги, датируется 1683-м годом ^2', в то время как математик XIX века Ямагути Кандзан, путевой дневник которого мы цитируем в главе 7, упоминает ещё более старую табличку, датировавшуюся 1668 годом и ныне утраченную. За два следующих столетия эти таблички появлялись по всей Японии, примерно 2/3 - в синтоистских святилищах, и 1/3 - в буддистских храмах. Мы не знаем, сколько их всего было изготовлено. Учитывая сангаку, упоминающиеся в математических текстах того времени, по крайней мере 1738 их были утрачены; более того, до наших дней дошло лишь 2% табличек, описанных в дневнике Ямагути. Поэтому резонно предположить, что изначально их было на много тысяч больше, чем те 900 табличек, которые сохранились до нашего времени. Практика вывешивания сангаку после падения сёгуната Токугава постепенно затихла, но некоторые поклонники продолжали вывешивать их и в 1980-е годы, и сангаку продолжают находить даже сейчас. В 2005 году в одной префектуре Тояма было обнаружено 5 табличек. "Новейшая" из них была обнаружена мистером Хори Ёдзи в святилище Убара, и датируется 1870-м годом. Две задачи в главе 4 взяты именно из этой таблички, и мы приводим её фото в разделе цветных изображений, рис.13.

Большинство сангаку содержит лишь конечный ответ на задачу; детальные решения даются редко. (В Священной Математике мы обычно приводим и ответы, и решения; многие - перерисованные из традиционных японских текстов.) В выставлении их на обзор присутствует и определённая бравада: "попытайся решить, если осмелишься!" Тем не менее, как Вы обнаружите сами, читая надписи к ним, дарители сангаку принимали, также, всерьёз и духовный, и даже религиозный аспекты этой практики, не видя ничего странного в предложении дощечек духам в обмен на прогресс в математике. Но кто же были эти создатели священной математики? Сангаку надписаны на языке, называющемся камбун, использующем китайские иероглифы и, в основном, китайскую грамматику, но включающий и диакритические пометки для обозначения японских смыслов. Камбун играл роль, аналогичную роли латыни на Западе, и его применение в сангаку указывало, что создатели этих задач имели хорошее образование. Фактически, большинство дарителей, видимо, принадлежало к классу самураев. В эпоху Эдо большинство самураев не имело занятий в сельской местности, с мечом в руке, зато они работали чиновниками правительства; многие стали математиками, и некоторые - известными. Тем не менее, надписи на табличках с очевидностью показывают, что сангаку создавались представителями всех классов; студентами, детьми, и иногда женщинами. Поэтому лучшим ответом на вопрос "Кто их создавал?" был бы: "все".

Созерцая этот урок, мы нарисуем более полную картину контекста, в котором сангаку создавались, с наивысшей возможной точки зрения, и с лёгким исследованием развития японской математики.

Эпоха математики

Ранняя история Японии неразрывно связана с Китаем, у которого она позаимствовала наибольшую часть своей культуры, буддистскую религию и систему правления. Верно это и для японской математики; однако данных о состоянии математики в Японии до VIII века у нас почти нет. Возможно, единственный определённый элемент информации об этих ранних временах состоит в том, что японцы имели некую порядковую систему обозначений, которую можно было использовать для записи высоких степеней десятки, аналогичную предложенной архимедом в его Исчислении песка. Согласно традиции, эта система использовалась до того, как легендарный Дзимму основал Японию в VII веке до н.э., однако вопрос о датировке и точной природе этой системы является открытым.

Более конкретная информация появляется лишь со времён эпохи Нара (710-794), когда ставка правительства была установлена в городе Хэйдзё, нынешний г.Нара, около Осаки. К тому моменту объединение Японии шло уже 4 века. Буддизм прибыл из Китая в середине VI века, и к VIII веку он набрал крайнюю мощь, свидетельством чего является То:дайдзи ("Великий Восточный Храм"), построенный в городе Нара в 752 году. В начале VIII века правители Нары открыли университет и перевели 9 китайских математических текстов, 6 из которых входили в число Десяти Классических. Наиболее известным из них был Цзю Жань Суаншу, "9 глав Искусства Математики". "Искусство математики" в этих девяти главах и других книгах состояло, в основном, в арифметике и элементарной алгебре; в Японии они служили, в основном, для помощи землемерам и сборщикам налогов. И хотя их полное влияние не было очевидно ещё примерно тысячу лет, эти китайские тексты заложили основу всей японской математики, и их важность нельзя недооценивать. Они, также, являются окном, проливающим свет на китайское общество того времени, и читатель может ощутить их вкус по задачам из этих влиятельнейших классических текстов в главе 2.

	Фото 1.5. "Великий Восточный Храм" Тодайдзи; построен в 752 г. н.э. в городе Нара, около Осаки. Сегодня это одно из самых популярных туристических мест в Японии. ((с) Todaiji)

Одно из влияний этих китайских текстов стало ощутимым уже в 718 году. В этот год правительство издало закон ёрё: рицурё:, дословно - "закон эры ёрё:" ², по которому было создано ведомство Сан Хакасэ, что значит примерно "Арифметические Сведения". Это Ведомство Арифметических Сведений состояло примерно из 70 функционеров среднего звена, в обязанности которых входило, видимо, измерение размеров полей и сбор налогов. По этому закону они были обязаны выучить математику из китайских книг в объёме, достаточном для исчисления налогов, и поэтому, хотя японцы и стали искусны в арифметических операциях, более серьёзная математика в то время не развивалась.

Вычисления в то время выполнялись с помощью набора маленьких бамбуковых счётных палочек, известных в Китае под названием суанзы, а по-японски - санги. Определённые конфигурации этих палочек представляли числа методом, схожим с представлявшимися чёрточками римскими цифрами на Западе. Работники Ведомства Арифметических Сведений, чтобы рассчитать налоги, ставили санги в клетки разлинованного кусочка бумаги, напоминвшего шахматную доску. С помощью набора определённых операций с ними они могли выполнять сложение, вычитание, умножение, деление и извлечение корней, что весьма напоминало по духу длительный способ выполнения деления студентами на Западе до изобретения калькулятора. (Цветное фото набора санги см. на рис.3.) В то время две японские религии, национальная - синтоизм, и недавно позаимствованная - буддизм, сосуществовали в относительном мире. В особенности буддистские храмы - как монастыри в те же века на Западе - стали хранилищами знаний. В главе 7 у Вас будет возможность посетить синтоистские святилища Исэ Дзингу: и Идзумо Тайся с математиком Ямагути Кандзаном в его путешествии по Японии для сбора задач сангаку. Посетил он и две великих буддистских комплекса Хо:рю:дзи и Тодайдзи, хотя они и не упоминаются в цитируемой нами части его дневника; в храме Тодайдзи в 752 году была сооружена крупнейшая в Японии статуя Будды. К храму было пристроено деревянное хранилище, в котором находилось большое число исторических документов, касающихся сбора налогов в эпоху Нара.

Эти документы, включающие карты и подписанные работниками Ведомства Арифметических Сведений, открывают некоторую утончённость в деле книгохранения, например, включавшего обширные отчёты инспекции провинции Суруга ³ за 738 год. Персонал Сан Хакасэ состоял из двух директоров, девяти младших директоров, шести чиновников, десяти клерков и сорока помощников. Первая группа, состоявшая из одного директора, одного чиновника, одного клерка и шести помощников, инспектировала одну деревню в течение двенадцати дней. Вторая, состоявшая из одного директора, трёх младших директоров, трёх клерков и двенадцати помощников, инспектировала 7 деревень и оставалась в каждой из них по 4 дня. Всего было 7 таких групп, все - различного состава, а общее число вовлечённых в это дело людей равнялось 1330. Всем директорам, младшим директорам и чиновникам ежедневно выделялось равное количество риса, соли и сакэ; клерки и помощники получали меньше. необходимы были существенные арифметические вычисления, чтобы определять общий объём отпускаемых им риса, соли и сакэ, и Ведомство Арифметических Данных проводило их с точностью.

Чтобы успокоить битвы различных сил, терзавшие Японию в эпоху Нара, в 794 году ставка правительства была перемещена в Хэйан-кё:, "город мира и спокойствия" - современный Киото. Хэйан-кё: оставался столицей до 1192 года, поэтому данная эпоха известна, как эпоха Хэйан. В эту относительно стабильную эпоху Япония начала развивать культуру, независимую от Китая, и систему письменности, независимую от китайской. Важнейшие достижения того времени были сделаны в сфере литературы: Сказание о Гэндзи леди Мурасаки Сикибу считается первым рассказом в мире, а дневник придворной жизни Сэй Сёнагон Записки у изголовья достиг мировой известности. Но из промежутка времени от эпохи Нара до XVII столетия до нас дошло совсем немного имён, связанных с математикой, и нет почти никаких свидетельств развития за 900 лет. Китайские тексты того времени вполне могли попасть в Японию, но, как и на Западе, духовенство мало интересовалось наукой и математикой, так что для математики это были "тёмные века".

От эпохи Камакура (1192-1333), когда правительство сёгуната располагалось в городе Камакура, вдали от Киото, осталось лишь небольшое количество упоминаний о санги, указывающих, что они применялись для арифметических вычислений. Например, в книге Камо-но Тё:мэй Хоссинсю (рассказы о буддизме), написанной около 1241 года и состоявшей из ста историй, есть 2 упоминания о санги. Одно - про подсчёт числа повторений в буддистском гимне, а в другом автор описывает дома, размётанные наводнением "как санги", ибо санги раскидывались по бумаге. В анонимных Удзи Сюи ("историях под редакцией министра Удзи") начала XIII века, одна из 197 юмористических историй повествует о человеке, который хотел научиться применять санги.

Столь скудные обрывки сведений приводят к заключению, что санги продолжали применяться для арифметических вычислений, но более серьёзная математика, видимо, не развивалась. Такое положение длилось всю эпоху Муромачи (1338-1573), название которой происходит от района Муромачи в Киото, в котором клан Асикага установил ставку. Как гласит история, в эту эпоху в Японии было сложно найти человека, знакомого с искусством деления. Тем не менее, это была не только эпоха интенсивной торговли Японии с Юго-Восточной Азией и появления богатых купцов, но и эпоха расцвета культуры. В это время, современное итальянскому Ренессансу, Канами Киёцугу (1333-1384) изобрёл драму Но, а его сын Дзэами Мотокиё (1363-1443) привёл его к пику развития. Через несколько столетий Сэн-но Рикю: довёл до совершенства чайную церемонию, являющуюся гораздо большим, чем просто чаепитие: даже сегодня миллионы японцев изучают этот ритуал, как путь к совершенствованию принципов Дзэн.

Как и на Западе, последние десятилетия XVI века в Японии были далеко не мирными. Сёгунат Асикага пал в 1573 году, когда военачальник Ода Нобунага (1534-1582) выгнал последнего сёгуна из Киото. В последующие десятилетия преемник Нобунаги, Тоётоми Хидэёси, с помощью Токугавы Иэясу, завоёвывал одну провинцию за другой, пока наконец в 1590-м году Япония не оказалась объединена. Когда это произошло, Нобунага и Хидэёси стали большими покровителями искусств и помогли создать основу для цветения культуры, которое вскоре и настало. Однако к концу этой жизни Хидэёси, видимо, начал вести себя ошибочным и опасным образом, заставив в 1591-м году своего друга и мастера чайной церемонии Сэн-но Рикю: совершить ритуальное самоубийство. Не удовлетворившись объединением Японии, на следующий год он устроил массивное вторжение в Корею, которое в итоге провалилось. Однако оно имело глубокие последствия для японской математики.

	Рис.1.6 Старейший соробан (счёты) в Японии. Он датируется примерно 1592-м годом н.э., и был во владении одного из солдат Хидэёси в порту Хаката ((с) Maeda Ikutokukai).

Один из солдатов Хидэёси в порту Наката, который этим военачальником был сделан базой вторжения, владел счётами, которые в Японии называются соробан и, очевидно, пришли туда из Китая. Этот солдатский соробан фактически является древнейшим в Японии из доживших до наших дней.

Были ли эти солдатские счёты действительно первыми, достигшими берегов Японии, или же нет, но процветавшая в то время торговля Японии со странами Азии неизбежно привела к импорту китайской суан фан, дословно - "счётной доски". В следующей главе мы обсудим развитие суан фан чуть детальнее. Её явление в виде соробана около 1592 года произвело в японской математике революцию; можно сказать, что традиционная японская математика и началась с появления этой счётной доски и с помощью мира, установленного сёгунатом Токугава.

Восход васан

О пришествии соробана в Японию также возвещает первая запись об идентифицируемом японском математике, Мо:ри Сигэёси ⁴, достигшем расцвета около 1600 г. О нём известно немного помимо того, что он жил в Осаке (пока этот город не был взят в 1615 году Токугавой Иэясу), после чего переселился в Киото. Сам Мо:ри привёз соробан из Китая, но в любом случае он был экспертом по его применению и сделал больше любого его современника для популяризации численных вычислений. В 1622 году Мори опубликовал небольшой начальный учебник Варидзансё, или "деление с помощью соробана". ⁵

	Рис. 1.7: Дзинко:ки 1715 года издания. Эта картина, отпечатанная на дереве, иллюстрирует преимущества использования счётов в деловых операциях. (Коллекция Фукагавы Хидэтоси.)
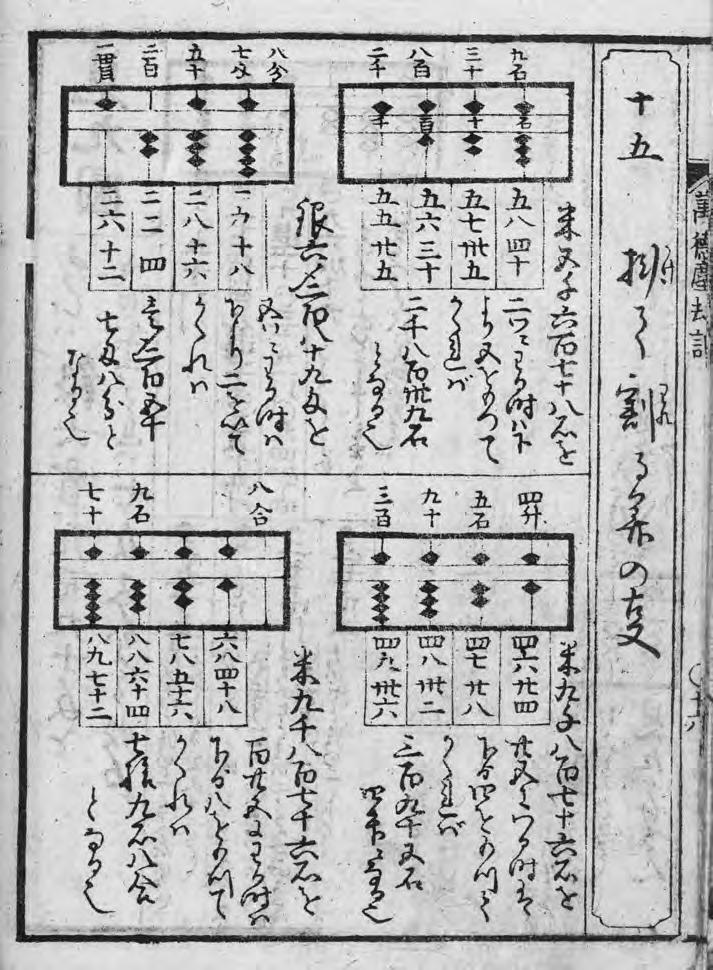
	Рис. 1.8: Пример вычиследний на соробане; позднее издание Дзинко:ки, 1818-1829 г. (Коллекция Фукагавы Хидэтоси)

Сам Мо:ри владел китайской книгой по соробану, известной Суанфа тонь зонь ("Системный Трактат о Математике") Чень Давэя, которая была опубликована в Китае в 1593 году, а в Японию попала вскоре после этого, другими словами - в то же время, что и сам соробан. Книга Ченя (см. главу 2) оказала большое влияние на японскую математику независимо от работы Мо:ри. Её японское издание было опубликовано в 1676 году Юаса Ичиро:дзаэмоном, но уже в 1620-е годы Ёсида Мицуёси(1598-1672) плотно переработал Суанфа тонь зонь, изменив задачи в ней на подходящие для Японии и добавив много иллюстраций. Таким образом родилась его Дзинко:-ки ("Большие и малые числа"), вышедшая в 1627 году и ставшая первой полной математической книгой, опубликованной в Японии.

Заглавие Дзинко:-ки происходит из старой религиозной книги XII века - Рё:дзин Хисё:, или "стихи тех дней". Дзинко:-ки Ёсиды в основном состояла из алгоритмов вычислений, для которых нынче мы используем калькулятор - таких, как извлечение квадратных и кубических корней. Эта книга тут же завоевала популярность, выдержав за три следующих столетия более трёхсот различных изданий: Новоя дзико:ки, Сокровище Дзико:ки, Богатства Дзико:ки и т.д. Конечно же, большинство из них было просто копиями, но Ёсида сам опубликовал не менее семи её версий. В версии 1641 года он предложил читателям для решения некоторые открытые проблемы. Когда читатели предлагали решения, он публиковал следующее издание. добавляя новые открытые проблемы и т.д. Таков был метод публикации многих математических книг в Японии: читатели вносили в них вклад своими решениями.

Одна из задач, рассматривавшихся в Дзинко:ки, состояла в вычислении числа π. В ответ математик Мурамацу Сигэкиё (1608-1695) опубликовал книгу Сансё ("математический склад"), в которой он с помощью правильного 2¹⁵=32768-угольника получил значение π=3.14159264877. Девятнадцатью веками ране Архимед уже вычислял значение π, вписывая в окружность правильный n-угольник и вычисляя длину окружности приближением периметра этого многоугольника. Чем больше сторон, тем точнее приближение и, соответственно, значение π ⁶. Мурамацу применил тот же самый приём, что и его современник Исомура Ёсинори (1640?-1710), который вычислил значение периметра 2¹⁷=131072-угольника, получив значение 3.141592664, но по некоторой причине опубликовал лишь 3.1416.

Самый знаменитый математик той эпохи, Сэки Такакадзу ⁷, тоже принял вызов в вычислении числа π. С помощью своего собственного метода, который был опубликован посмертно его учениками в книге 1712 года Кацуё: Санпо: ("Коллекция важных математических результатов"), он получил значение π=3.14159265359, правильно вычислив 11 его значащих цифр. Такэбэ Такахиро (1664-1739, ученик Сэки, получил точное значение 41 знака π. В силу их важности, мы посвятили немалую часть главы 3 книге Дзинко:-ки и различным вычислениям π.

Начало традиционной японской математики обычно датируется публикацией Дзинко:ки в 1627 году. Девять глав "Суждений" Ченя и другие классические китайские произведения продолжали оказывать влияние на японскую математику - как прямое, так и через переводы, но с установлением сакоку развитие японской математики быстро стало независимым от Китая. Однако странно то, что Дзинко:ки не привела к немедленной смерти санги. Соробан быстро заменил санги в повседневных деловых вычислениях, но он не столь хорошо подходил для сложных алгебраических операций, в частности - решения уравнений высших степеней, к которым японские математики весьма пристрастились. В результате, санги отлично сосуществовали параллельно с соробаном и в XIX веке.

Главной проблемой для мира в эпоху Эдо были самураи. Века военных столкновений превратили их в малообразованных дикарей, которым надо было усмириться и цивилизоваться. Токугава приложили в этом направлении много усилий, в результате которых за несколько поколений самураи превратились в высокообразованный класс, грамотный и изощрённый в искусных аспектах жизни, как благородные европейцы того же времени. Надо сказать, что большинство этих воинов, потеряв свои работы, стали обычными гражданскими служащими. На 3-4 дня в неделю самураи могли отправляться на работу в провинциальный замок, но оплата там была столь ужасна, что часто им приходилось брать работу со стороны. ⁸ Университетов в эпоху Эдо в Японии не было. Поэтому многие самураи были светилами в качестве учителей в маленьких частных школах, называвшихся дзюку, которые были посвящены чтению, писанию и арифметике; последнее означало умение пользоваться соробаном. В то время, как в предыдущие эпохи самураи посещали деревни для набора рекрутов, теперь их визиты стали реже, и крестьяне столкнулись с необходимостью измерять площади их полей самостоятельно. В результате, они тоже начали посещать дзюку, что было возможно благодаря низкой плате за обучение. С притоком всех людей из замков, от богатых до бедных, дзюку расцвели. Расписание одной из школ, дзюку Ё:кэн, показывает, что её курсы за 50 лет посетили 2144 студента, многие из которых были взрослыми. Их учителем был математик Сакума Ё:кэн (1819-1896), и эта маленькая деревянная школьная комната сохранилась до наших дней. Недавнее исследование ⁹ показывает, что в XIX веке, в конце эпохи Эдо, в Японии существовало около 80.000 дзюку. И хотя, как и на Западе, дети считались рабочими, а не студентами, доморощенное обучение, ведомое дзюку, вылилось в уровень грамотности, в высшей степени сравнимый с уровнем других стран того времени.

Рис. 1.9: дзюку Ё:кэн, в которой математик Сакума Ё:кэн (1819-1896) за 50 лет обучил 2144 студента. (город Тамура)

Многие математики, обычно - самураи, получившие лицензию "Учитель математики", посещали эти сельские школы, чтобы обучать математике - и, очевидно, большему, нежели просто арифметике. И именно из этих островков, изолированных от Запада и всё более удаляющихся от Китая, возникла васан, дословно - "японская математика" ^3'. Обычные люди в дзюку, не имевшие возможности публиковать свои собственные книги, использовали древний обычай принесения табличек с обетами в храмы, и начали подвешивать сангаку, делая таким образом одновременно и религиозное подношение и рекламу своих результатов. В итоге, они создали великолепное искусство.

Сангаку были не единственным посредником в распространении геометрии. Корейцы начали печатать книги с наборным шрифтом за 100 лет до Гуттенберга ¹⁰, и как корейские, так и европейские типографии проникли в Японию до начала XVII века. Однако, как упоминалось, самым излюбленным методом производства книг в Японии стала печать деревянными дощечками на рисовой бумаге, и к концу XVII века начало появляться изобилие математических текстов, многие из которых содержали задачи, идентичные находимым на сангаку или взятые из них. Иногда в этих текстах предлагались и решения, не написанные на табличках, и в данной книге мы часто цитируем их в разделе ответов. Многие из иллюстраций Священной математики также взяты прямо из книг на рисовой бумаге, изначально напечатанных в XVII-XIX веках.

Таким образом, к концу XVII века васан, традиционная японская математика, прочно установилась. Однако понадобились два последующих столетия, чтобы её традиционные методы принесли свои наиболее ошеломляющие и оригинальные результаты.

Расцвет и закат васан

В XVIII и XIX веках, с углублением изоляции Японии, было опубликовано наибольшее число текстов васан, доказаны наиболее интересные теоремы и создано большинство задач сангаку.

Большинство результатов, полученных в васан, не были прорывами по стандартам Запада, частично - потому, что Япония так и не развила полностью оперившуюся теорию исчислений. Математики васан находили площади и объёмы геометрических фигур в основном теми же методами, что и Евдокс и Архимед в античной Греции (и в основном так же, как мы это делаем сегодня численно, с компьютерами). Например, окружность можно разделить на прямоугольные полоски, как на рис. 1.10. Чем уже эти полоски, тем ближе сумма их площадей к площади круга. Эта идея служила основой энри - широкого термина со значением "принцип круга", который студентам, знакомым с исчислениями, известен, как определённое интегрирование. Как известно студентам, существует несколько методов вычисления площадей геометрических фигур разрезанием их на ломти подходящим образом и устремлением толщины ломтиков к нулю. Для каждой ситуации это можно делать неформально, не доказывая теорем о пределах, ненавистных студентам, но отсутствие этих теорем, в частности - первой и второй фундаментальной теоремы исчислений, ограничивает в обращении с определёнными интегралами и не позволяет создать теорию для интегрирования в целом, т.е. производить неопределённое интегрирование. Такова, в той или иной степени, и была ситуация в васан. Детальнее мы обсудим это в главе 9.

Несмотря на эти недостатки, васан нельзя обвинить в недостатке изобретательности. Сэки развил теорию определителей до Лейбница, а другие японские геометры доказали ворох известных теорем раньше своих западных коллег или, по меньшей мере, независимо от них. С некоторыми из них мы встретимся в главе 8. Они включают: Теорему Декарта об окружности, задачу Мальфатти, Теорему Casey, the Soddy hexlet и некоторые другие.

Вдобавок, японцы были весьма искусны в обращении с уравнениями высших степеней. Мы имеем в виду именно высшие степени. В дневнике Ямагути мы рассмотрим знаменитую проблему - Задачу храма Гион, в которой фигурирует уравнение 1024-й степени. (А студенты боятся квадратных!) ^4' Математик Адзима Наонобу (1732-1798) стал знаменитым благодаря её сведению к уравнению 10-й степени ¹¹, которое затем было решено численно. Адзима доказал большое число сложных геометрических теорем, которые мы обсудим в главе 3, а также ближе всех японских математиков подошёл к созданию полной теории определённого интегрирования.

Рис. 1.10: Из книги Савагучи Кадзуюки 1671 года Кокон санпо:ки ("Старая и новая математика"): иллюстрация, как приближать площадь круга, нарезая его на прямоугольные полоски. На первом году курса исчислений площадь круга вычисляется точно так же - разрезанием круга на полоски и устремлением суммарной площади полосок к пределу, когда их толщина стремится к нулю. (Университет образования города Аити) /требуется вставка/

Работа Адзимы построена на работе его предшественника Мацунага Ёсисукэ (1692?-1744), изучавшего бесконечные ряды и их применение к вычислению площадей путём интегрирования. За ними последовал Вада Ясуси (1787-1840), который жил в нищете и создал большое количество табличек по определённым интегралам. Учида Кё: (1805-1882) изучал интегрирование в дзюку Вады. Далее он написал серию книг, в которых рассматривалось интегрирование тел, включая пересечения цилиндров, сфер и т.д. С задачами этого сорта Вам будет предложено сразиться в главах 5 и 6.

Как мы уже сказали, многие задачи сангаку появились и в традиционных японских текстах. Фудзита Садаскэ (1734-1807) опубликовал книгу Сэйё: сампо: ("Математика в деталях"), а его сын Фудзита Кагэн (1772-1828) продолжил эту традицию публикацией Симпэки сампо:, что иногда переводится как "Математика святилищ и храмов", а иногда - как "Священная математика", первый сборник задач сангаку. (Портрет Фудзиты Кагэн см. на рис.14.) Эти работы служат источником некоторых знаменитых задач, появляющихся и в нашей книге.

С ходом веков в Японию, через Китай и голландцев в Нагасаки, проникло небольшое число намёков на западную математику. Например, очевидно, что японцы узнали о логарифмах из китайской публикации 1713 года Су-ли Чинь-ин. Однако даже в 1824 году японские математики, похоже, с удивлением восприняли в голландской работе изображение эллипсографа - механизма для рисования эллипса, известного на Западе со времён Леонардо да Винчи. С середины XIX века появляются рукописи, содержащие одновременно и восточную, и западную нотацию.

Но васан удерживала свои позиции до тех пор, пока, вследствие открытия Японии Западу Коммодором Пэрри, клан Токугава не потерял власть в 1868 году. Новое правительство Мэйдзи решило, что для превращения Японии в равного партнра для зарубежных наций она должна быстро модернизироваться. Их программа включала и математику. По всей Японии были установлены правительственные школы, и в Гакурэй - "Фундаментальном Законе об Образовании" от 1872 года - лидеры Мэйдзи объявили, что "в школах больше не будут учить васан, а только западную математику".

Благодаря дзюку, математика в Японии цвела, поэтому ввести ёсан ("западную математику") оказалось легко, и она была быстро принята. Конечно, "твердолобые" защищались. Один из последних самураев, Такаку Кэндзиро: (1821-1883), написал: "Астрономия и физические науки, какими они предстают на Западе, - поистине вечны и неизменны, и им мы должны учиться; но что касается математики, то тут Япония - мировой лидер". ¹² Под конец сопротивление стало напрасным. С Фундаментальным Законом Мэйдзи учителя традиционной математики потеряли свою работу, и васан было предначертано исчезнуть. С узко математической точки зрения её смерть, возможно, не следует чрезмерно оплакивать, но с эстетической точки зрения мы несомненно что-то потеряли, когда в результате любители традиционной математики перестали создавать свои прекрасные задачи и таблички, которые они предлагали миру. Мы можем быть благодарны лишь за то, что от них осталось.

Глава 2. Китайские корни японской математики

	Рис. 2.1: Изображение человека, измеряющего высоту дерева с помощью простейшей тригонометрии; взято из издания Дзинко:-ки, опубликованного между 1818 и 1829 годами. Как и большинство задач в Дзинко:-ки, происходит из китайских источников.

Я слышал, что Великий Префект сведущ в искусстве чисел, поэтому да будет мне дозволено спросить Вас: во времена старого Фу-хси было измерено небо и установлен календарь. Но нет шагов, которыми можно взойти на небо, а землю не измерить ногами. Мне хочется спросить, каковы истоки этих чисел? - из "Чжоу би суан цзинь".

Чтобы понять развитие японской математики, надо оценить китайскую математику, которая столь сильно на неё повлияла. В этой главе мы дадим краткий обзор древней и средневековой китайской математики, и представим некоторые задачи из классических китайских текстов. Эти задачи интересны не только тем, что они показывают состояние китайской математики в прошедшие века, но и потому, что они предлагают дразнящий взгляд на общество, ежедневная жизнь которого вращалась вокруг риса, лошадей, бизнеса и счётов. Для решения этих задач иногда требуются трюки, но в большинстве своём они не представляют сложности для учащихся средней или высшей школы.

Самая ранняя из великих математических книг - это Чжоу би суан цзинь, или, в вольном переводе, "Классика арифметики гномона и круговой путь небес". Автор и дата этой книги нам неизвестны. Все очевидные факты указывают на то, что учёные с ходом веков делали добавки к её оригиналу. Известный диалог в начале этой книги происходит между принцем Чжоу-Конь и его учёным министром Шань Као. Чжоу-конь умер в 1105 году до н.э., но его появление в роли участника данного диалога указывает не столько на дату создания оригинала, сколько на поэтическую вольность. Большинство учёных верит, что эта книга была написана во втором-третьем веке до н.э., хотя в некоторых недавних исследованиях и выдвинута гипотеза, что её создание не было закончено до 1-го века н.э. 1 С точки зрения современного студента, Чжоу би - не математический текст. Математической нотации в нём практически нет, а большинство концепций изложено словами. В нём есть дискуссия о гномоне (солнечных часах) - палке, вертикально воткнутой в землю, тень которой использовалась для измерения высоты солнца. В целом, речь в Чжоу би по большей части идёт об астрономии и создании календаря; включены туда и карты звёзд около небесного Полюса.

С другой стороны, в Чжоу би есть дроби, обсуждается их умножение и деление, и хотя извлечение квадратного корня чётко не проработано, текст делает очевидным, что использовались и квадратные корни. Для нас величайший интерес представляет то, что в начале этой книги, в диалоге между Чжоу-Конь и Шань Као, присутствует дискуссия о треугольнике со сторонами 3,4 и 5. И хотя она изложена трудным языком, очевидно, что китайцы понимали Теорему Пифагора: что сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы. Но общего доказательства этой теоремы там нет. Эта часть Чжоу би считается старейшей и датируется примерно 6-м веком до н.э. - примерно тем же временем, когда Пифагор, как говорят, открыл эту теорему в Греции.

	Рис. 2.2: Это изображение из Чжоу би суан цзинь показывает, что китайцы давно понимали теорему Пифагора, хотя общего её доказательства и не давали.

С нашей точки зрения, более существенной работой является Цзю Жань Суаншу, или "9 Глав Искусства Математики". Автор и дата этой книги опять-таки неизвестны, хотя большинство экспертов, похоже, верит, что она была завершена во II-III вв. н.э. Девять глав Цзю Жань содержат в целом 246 задач, касающихся межевания, инженерии, сбора налогов и других тем, требующих дробей, геометрической и арифметической прогрессий, и решения систем уравнений. Восьмая глава, в зависимости от её датировки, возможно, содержит первое в истории упоминание об отрицательных числах, а в девятой - Гоу гу, или "Ширина и высота прямоугольных треугольников" - представлены 24 задачи по Теореме Пифагора. Некоторые из них мы далее приведём. Эта глава содержит, также, раннюю формулировку квадратного уравнения и формулу для его решения. Возможно, не самую раннюю, поскольку, согласно некоторым историкам, египтяне начали изучать квадратные уравнения до 2000 г. до н.э.

Стоит заметить, что хотя мы и говорим о "девяти главах" как о "книге", её содержание было, видимо, записано на бамбуковых дощечках размером 2×25 см. В июле 2002 года японские газеты сообщили об извлечении из земли примерно 20.000 деревянных и бамбуковых дощечек, датирующихся 221-206 гг. до н.э.; на некоторых из была написана таблица умножения. Датировка делает их современниками старейшей версии Чжоу би суан цзинь. И хотя бумага вошла в Китае в оборот около 105 г. н.э., похоже, что и более поздние версии "девяти глав" были "изданы" на бамбуке.

Цзю Жань Суаншу была самым влиятельным из древних китайских текстов, лидируя среди множества других книг, приобретших за века свою собственную славу. Одной из них была Сунцу Суанцзинь, или "Классическая арифметика Сунцу". (Этого Сунцу (часто, Сунзи) иногда путают с известным стратегом, автором классической военной книги "Искусство войны", но считается, что стратег жил в VI-IV веке до н.э., в то время как математик Сунцу, вероятно, работал в V веке н.э.). В период с 618 по 901 г. н.э. книги Чжоу би, Цзю Жань и Сунцу, наряду с семью другими, считались правительством Китая учебниками, а между 1078 и 1085 г. они были опубликованы вместе, под названием "Десять Классических [книг]".

В XIII веке в Китае появилось ещё несколько важных книг. Одна из них, Шушу Цзючжань или "Математические рассуждения в 9 главах" Цин Цзюшао 1247 года, содержит "основу измерения небес" - символ "1", а также символ нуля, и чёткое различие между положительными и отрицательными числами. И хотя её название и схоже с названием тех, первых, "девяти глав", эти "9 глав" Цина Тюшао - совсем не то же самое. Ещё большую важность для васан представило "Суансюэ Цымэнь", или "Введение в математические исследования" Чжу Шицзе 1299 года, из которой мы также приведём некоторые задачи.

Как уже говорилось в главе 1, в начале VIII века японское правительство сделало "9 глав" и 8 других математических текстов основой университетской системы обучения математике. До XVII века в Японию могли, также, попасть и некоторые более поздние книги, но, так или иначе, свидетельств тому немного. Лишь ко времени заимствования китайских счётов суан фан информация становится более определённой. Истоки суан фан также скрыты во мгле и являются предметом споров. Первое полное современное описание "счётной доски" можно найти в Суанфа тонь зонь, или "Системный трактат о математике" Чень Давэя 1593 года. Столь поздняя дата привела некоторых историков к той точке зрения, что счёты были неизвестны в Китае до относительно недавнего времени, но есть и другие убедительные описания от 1513 и 1436 года, и даже от VI века и более ранние. Изображение суан фан было опубликовано в китайской математической книге Куйбэн дюсянь сиян зази ("Главная книга четырёх слов в стихах") 1371 года ², поэтому очевидно, что к этому времени счёты уже сформировались. Имеет основания и гипотеза, что счётные палочки суанзы, упоминавшиеся в главе 1, постепенно превратились в счёты.

"Трактат" Чень Давэя оказал большое воздействие как на китайскую, так и на японскую математику. Сам Чень (1533-1606) был местным правительственным работником, который должен был знать, как использовать суан фан, и в начало своей книги он включил две главы по основам вычислений и применению счётов. Девяти главам своей книги он последовательно дал те же имена, что и у девяти глав Цзю чжань суаншу, хотя у Ченя в них вошли магические квадраты, музыкальные трубы, изложенные в стихах формулы и, практически, всё, о чём он только думал. Эта книга веками оставалась популярной в Китае, и была издана даже в 1964 году, когда старые люди всё ещё могли цитировать формулы в стихах ³.

При такой популярности в Китае неудивительно, что вскоре книга Ченя изменила и направление японской математики. Мы уже увижели, что "Трактат" привёл прямо как к "Делению с помощью соробана" Мо:ри Сигэёси, так и к феноменально успешной Дзинко:ки Ёсиды. Влияние "Трактата" Ченя, как и других китайских классиков, продолжалось и до XIX века. В 167 году Юаса Ичиро:дзаэмон опубликовал японскую версию "Суждений". Через 20 лет, в 1658-м, Хадзи До:ун опубликовал японскую версию "Введения" Чжу Сицзе 1299 года, а в 1690-м Такэбэ Катахиро (1664-1739) опубликовал эту же работу в расширенной версии. Он назвал её Сангаку Кэймо: Гэнкай Тайсэй, или "Комментарии к Суансюэ Цымэнь". Лишь в 1824 году японский математик Китагава Мо:ко (1763-1833) вознамерился издать перевод оригинальной Цзю Чжань, но эта попытка потерпела провал, и от неё осталась лишь рукопись.

Чтобы лучше передать вкус этих великих китайских работ, которые до сих пор не особо известны на Западе, мы представим здесь некоторые задачи из них. От одного автора к другому явно имеет место определённое количество наследования. Мы исключили большинство повторов, но среди этих задач всё ещё осталась некоторая схожесть, отражающая скорее многовековую практическую реальность, чем изъян редактирования. Вы, также, отметите, что названия глав не всегда точно соответствуют одержанию задач. Когда ответы не приводятся вместе с задачами, их можно найти в конце главы.

1. Цзю чжань суаншу, или "9 глав искусства математики"

В целом 9 глав этой известной книги содержат 246 задач. Мы представим по одной задаче из каждой главы. Большинство из них очень легки, и мы надеемся, что они не представят особой сложности для современных студентов. Взгляд на форму решений, которые обычно содержат дроби, помогает понять, что в древней китайской математике дроби использовались исключительно для представления нецелых чисел; десятичных дробей не было.

Задача 1-1. (из главы 1 Цзю Чжань, "Об измерении различных полей")
Обойдя круглое поле, мы нашли длину его окружности равной 181 бу (=208.15 м.), а диаметра - равным (60 + 1/3) бу (= 69.38 м.) Найти значение π, равное отношению длины окружности к диаметру, и площадь этого поля в форме дроби ⁴.

Решение: Поскольку π = 181 / (60+1/3) = 3, площадь равна A = πr² = 3*(181/6)² = 32761/12 = 2730 + 1/12 бу = (11 + 90/240) се + 1/12 бу = 11 се + (90 + 1/12) бу.

В своём обзоре "Девяти глав" 263-го года н.э. комментатор Лю Хуэй (220-265?) отметил, что значение π = 157/50 = 3.14 лучше, чем 3. Ёсида цитирует в своей Дзинко:-ки другую задачу из главы 1 "Девяти глав", которую мы приводим как задачу 1 в главе 3 данной книги.

Задача 1-2. (из главы 2 Цзю Чжань, "Пропорции")
В целом, при честном обмене за 50 сё: проса дают 27 сё: риса. Есть 21 сё: проса. Сколько сё: риса мы за него получим взамен? (решение)

Задача 1-3. (из главы 3 Цзю Чжань, "Распределение")
Некая женщина искусна в ткачестве. В первый день она соткала некое количество ткани, во второй день - вдвое больше, в третий - ещё вдвое больше, и т.д. В целом, за 5 дней она соткала 5 сяку ткани. Сколько она соткала за первый день?
Эта задача цитировалась и в более поздней Сунцу Суанцзинь. (решение)

Задача 1-4. (из главы 4 Цзю Чжань, "О подсчёте площади поля")
Пусть площадь прямоугольного поля A = 240 бу, причём его ширина равна x бу, а длина - y бу. ⁵ Для каждого данного ниже x найдите y в виде дроби.

1. x = 1
2. x = 1 + 1/2
3. x = 1 + 1/2 + 1/3
4. x = 1 + 1/2 + 1/3 + 1/4
5. x = 1 + 1/2 + 1/3 + 1/4 + 1/5
6. x = 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 (решение)

Задача 1-5. (из главы 5 Цзю Чжань, "О значении некоторых объёмов")
Рядом с рекой возводится земляная насыпь, 127 сяку в длину и 4 сяку в высоту, ширина которой с нижней [по течению] стороны равна 20 сяку, а с верхней - 8 сяку.

1. Найти объём этой насыпи.
2. За зиму один рабочий может перенести 444 кубических сяку земли. Сколько рабочих надо, чтобы построить эту насыпь за один сезон? (решение)

Задача 1-6. (из главы 6 Цзю Чжань, "Оплата")
Однажды один путешественник отправился в путешествие, взяв с собой несколько кин ⁶ для уплаты налогов. В пути ему пришлось пройти через 5 точек сбора налогов: A, B, C, D и E. Проходя через A, он заплатил половину от того, что взял. Проходя через B, он заплатил треть от того, что у него осталось. В точке C он заплатил четверть того, что у него осталось после B, и аналогично послупил в точках D и E. В результате, в целом он заплатил 1 кин налогов. Сколько денег для уплаты налогов было у него в самом начале? (решение)

Задача 1-7. (из главы 7 Цзю Чжань, "Избыток и недостаток")
Дынная плеть растёт на 7 сун в день. Плеть вьюнка растёт на 10 сун в день. В один и тот же день дынная плеть начинает расти вниз с вершины скалы высотой в 90 сун, а вьюнок - вверх с её подножия. Через сколько дней они встретятся? (решение)

Задача 1-8. (из главы 8 Цзю Чжань, "Квадрат", или "О системах линейных уравнений")
Предположим, что каждая грядка рисовых полей A, B и C даёт по a, b и c то риса соответственно. Пусть общий урожай трёх грядок A, двух грядок B и одной грядки C равно 39 то; общий урожай двух грядок A, трёх грядок B и одной грядки C равен 34 то, а общий урожай одной грядки A, двух грядок B и трёх грядок C равен 26 то. Найти a, b и с. (решение)

Задача 1-9. (из главы 9 Цзю Чжань, Гоу гу, или "Правильные треугольники")
Бамбуковый стебель высотой в 10 сяку был сломан в точке Q так, что его вершина упала и коснулась земли в точке T. Расстояние от его корня P до T равно 3 сяку. Найти длину PQ.

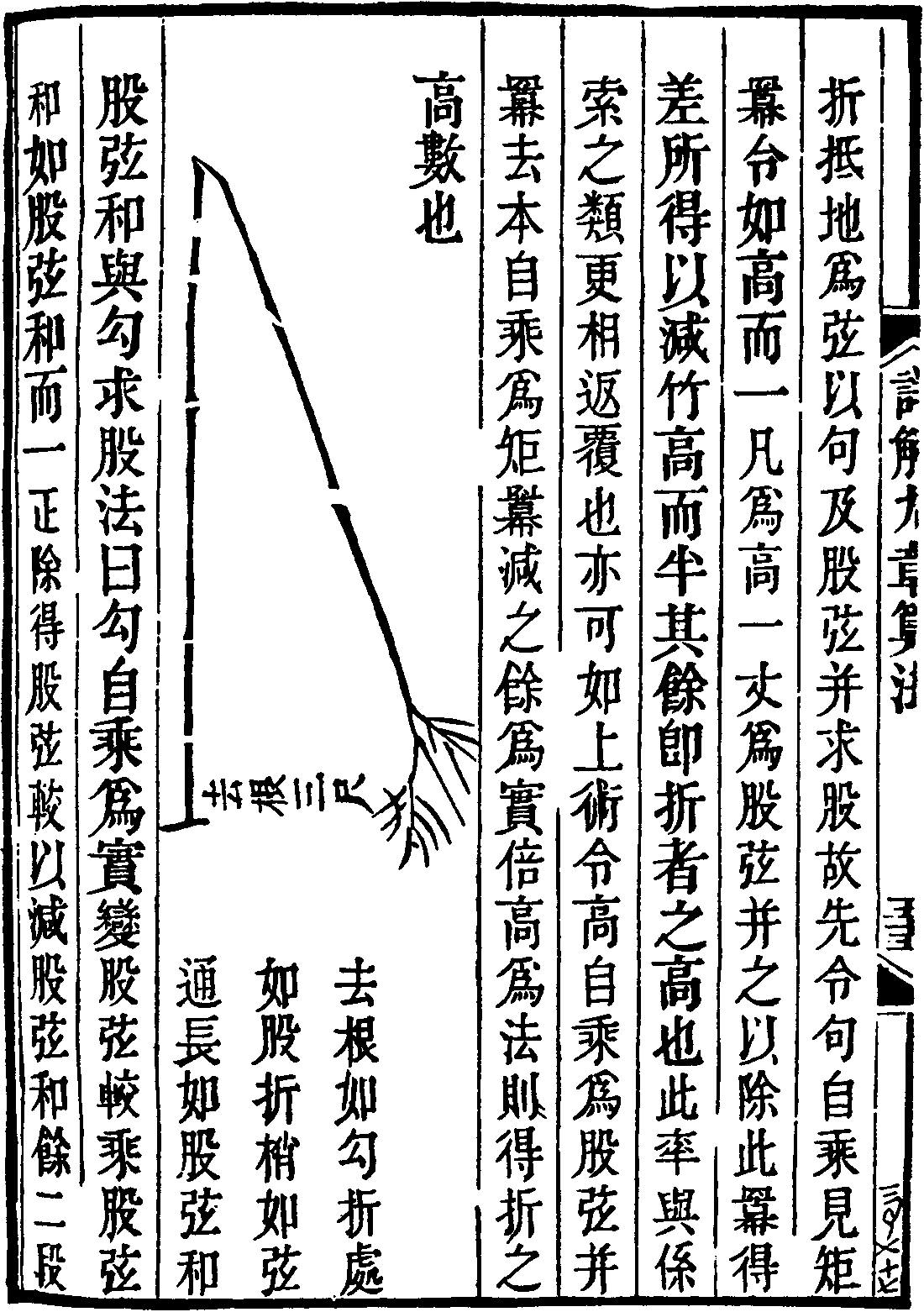
Рис. 2.3. Иллюстрация теоремы Пифагора на сломанном стебле бамбука: эта знаменитая задача из "9 глав" была опубликована во множестве следующих книг. Версия, приведённая здесь, взята из книги Ян Ху Сяньцзи Цзючжань Суанфа 1261 года.

После Цзю Чжань эта знаменитая задача появилась во множестве китайских книг, включая Сяньцзи Цзючжань Суанфа Янь Ху, 1261 года н.э., и Суанфа тонь зонь Чень Давэя 1593 года.

Ответ следует прямо из теоремы Пифагора: если длина PQ равна x, то x² + 3² = (10-x)². Решение этого уравнения даёт x = 91/20 = 4 + 11/20 сяку.

2. Сунцу Суанцзинь, или "Классическая арифметика Сунцу", V век н.э.

В момент написания книга Сунцу состояла из трёх томов. Первый был полон задач по элементарной арифметике, которые мы здесь не приводим. Однако мы приведём полдюжины интересных задач из второго и третьего томов. Одна из них - знаменитая "Китайская теорема об остатках", которую мы приводим ниже в качестве задачи 2-6.

Задача 2-1.
Мы строим земляную насыпь 5550 сяку длиной и 38 сяку высотой, одна из сторон которой равна 20 сяку, а другая - 54 сяку. Рабочий может перенести 300 кубических сяку грунта за сезон. Сколько рабочих требуется для постройки этой насыпи?
Как видите, эта задача взята из Цзю Чжань (задача 1-5 выше), и решается так же. (решение)

	Рис. 2.4. Безжалостные воры, крадущие рулон шёлка, появились в Дзинко:-ки в 1643 году, но эта задача была взята из Сунцзу Суанцзинь.

Задача 2-2.
Воры украли со склада длинный рулон шёлковой ткани. В кустах, вдали от склада, они измерили его длину. Если каждый вор получит по 6 хики, то у них останется 6 хики, а если каждый вор возьмёт по 7 хики, то последнему вору вообще ничего не достанется. ⁷ Найдите число воров и длину ткани.
Ответ: Пусть N - число воров, а L - длина ткани, тогда первое условие говорит, что 6N = L-6, а второе - что L = 7(N-1). решение этой системы уравнений даёт N = 13 человек и L = 84 хики.
Эта задача про воров шёлка появляется и в Дзинко:-ки Ёсиды 1631 года.

Задача 2-3.
Хочется измерить высоту дерева, дающего тень в 15 сяку Около дерева мы втыкаем маленькую палочку, 1.5 сяку высотой, и её тень оказывается равной 0.5 сяку. Найдите высоту дерева.
Эта задача тоже появляется в оригинальной Дзинко:-ки от 1627 года. (решение)

Задача 2-4.
В загоне есть несколько петухов и кроликов. Общее число их голов равно 35, а лап - 94. Сколько в загоне петухов, и сколько кроликов?
Петухи и кролики появились в Инки санка 1640-го года (в главе 3) и, как вороны и черепахи, в японской книге 1815 года Сампо: тэндзан синанроку Сакабэ Ко:хана (1759-1824). (решение)

Задача 2-5.
Сверху от ворот есть 9 валов; на каждом валу растёт по 9 деревьев, у каждого из которых по 9 ветвей. На каждой ветви по 9 гнёзд, а в каждом гнезде живёт по 9 взрослых ворон, и у каждой из них по 9 птенцов. У каждого птенца по 9 перьев, и каждое перо имеет по 9 цветов. Сколько всего деревьев, веток, гнёзд, ворон, птенцов, перьев и цветов? (решение)

Задача 2-6. (Китайская теорема об остатках)
Есть неизвестное число объектов. Если их разложить по три, то останется два; если их разложить по 5, то останется 3, а если их разложить по 7, то останется 2. Каково число объектов?

Это прототип известной задачи, появлявшейся во многих руководствах мира. Её типичная средневековая версия звучит так: "Старуха пошла на базар, лошадь наступила на её корзину и разбила яйца. Всадник предложил возместить ущерб, и спросил, сколько яиц она несла. Она не помнила точно их число, но когда она брала их по два, оставалось одно. То же самое происходило, когда она брала их по три, по четыре, по пять и по шесть, но когда она брала их по семь, ничего не оставалось. Какое наименьшее число яиц могло у неё быть?" ⁸

Версия Сунцу важна потому, что она предлагает метод решения, эквивалентный тому, что даётся в курсе современной теории чисел. Его оригинальное решение ⁹ выглядит примерно так:

Ответ: 23.
Решение: Если их брать по три, останется два: положим, 140. Если их брать по пять, останется три: положим, 63. Если их считать по семь, останется два: положим, 30. Взяв сумму этих [трёх чисел], получим 233. Вычтем из неё 210 и получим ответ.
В общем случае: Остаток при счёте по три умножим на 70. Остаток при счёте по пять умножим на 21. Остаток при счёте по 7 умножим на 15. Пока [сумма получившихся чисел] больше или равна 106, будем вычитать из неё 105, и таким образом получим ответ. ^5'

Приложение общего правила к данному случаю приводит к ответу 2*70 + 3*21 + 2*15 - 210 = 23.

Расшифруем описание Сунцу. Если есть N объектов, то "считать их по три" означает просто вычитать по 3, пока, в данном случае, не останется 2. Другими словами, N при делении на 3 даёт остаток 2. Студенты курса алгебры знают более изощрённое выражение этого факта: N = 2 (mod 3) (читается, как "N равно 2 по модулю 3"). В общем случае, x = r (mod m) означает, что x при делении на m даёт остаток r. ^6' Например, 38 = 2(mod 12), так как 12 входит в число 38 три раза с остатком 2. Аналогично, 50 = 2 (mod 12), поскольку 12 входит в 50 четыре раза с остатком 2. В задаче Сунцу:

N = 2 (mod 3),
N = 3 (mod 5),
N = 2 (mod 7).        (1)

Таким образом, на современном языке задача заключается в решении системы из трёх сравнений. Может найтись (и в данном случае, определённо, так оно и есть) более чем одно N, удовлетворяющее трём этим соотношениям, но предполагается, что нам нужно наименьшее.

Мы будем искать решение весьма прозаично. Отметим, что первое число в описании Сунцу равно 2*70 = 140 = 2 (mod 3). Отметим, также, что 140 + 63 = 2 (mod 3) и 140 + 63 + 30 = 2 (mod 3). Аналогично, 63 = 3 (mod 5), но поскольку и 140, и 30 делятся на 5, 140 + 63 + 30 = 3 (mod 5). Наконец, 30 = 2 (mod 7) = 140 + 63 + 30.

Таким образом, сумма N = 140 + 63 + 30 = 233 удовлетворяет всем трём сравнениям. Но 233 - не наименьшее из таких N. Наименьшее общее кратное 3, 5 и 7 равно 105, и 2*105 = 210 тоже делится на все эти три числа. Таким образом, мы получаем ответ Сунцу N = 233 - 210 = 23. Последний шаг был именно тем, о чём говорилось: "пока [сумма получившихся чисел] больше или равна 106, будем вычитать из неё 105"; фактически, мы вычли наименьшее кратное 105.

Несомненно, Вы поинтересуетесь, откуда Сунцу взял числа 2*70, 3*21 и 2*15. Эта часть требует некоторых продвинутых предположений. Сначала мы умножили делители двух последних соотношений из (1), получив 5*7=35. Затем мы стали искать число, кратное 35, и удовлетворяющее первому сравнению. Очевидно, что число 140 - таково. (Вы можете заметить, что число 35 и само таково; объясните, почему это решение нам не нужно.) Далее мы ищем число, кратное 3*7=21 и удовлетворяющее второму сравнению, и число, кратное 3*5=15 и удовлетворяющее третьему сравнению. Вот откуда взялись числа Сунцу.

Задача Сунцу появилась в Дзинко:-ки издания 1631 года, в котором она называлась задачей "извлечения 105".

3. Суансюэ Цымэнь, или "Введение в математические исследования", Чжу Шицзе, 1299 г.

Как уже упоминалось во вступлении к этой главе, японский математик Хадзи До:ун опубликовал японскую версию этой важной книги в 1658 году. Оригинальная китайская версия состояла из трёх томов, и содержала 259 задач.

В томе 1 автор обсуждает различные оценки числа π. Чжу Шицзе упоминает оценку π=3 как "старое π", и даёт краткий очерк некоторых продвижений в вычислении π в течение веков. Он упоминает математика Лю Хсина, который использовал значение 3.154 в первом десятилетии первого века н.э., хотя записи о том, как он к этому значению пришёл, и не сохранилось. ¹⁰

Чжу Шицзе цитирует, также, Лю Хуя, который в 263 г. н.э. с помощью 192-угольника получил значение π = 157/50 = 3.14 (см. задачу 1-1).

В V веке Зу Чоньжи и его сын Зу Гэнь получили оценку 3.1415926 < π < 3.1415927. Хотя Чжу Шицзе и не описывает эту работу в делалях, впоследствии математики подтвердили точность результата Зу с помощью 16384-угольника. И лишь примерно к 1600 году европейские оценки π приблизились к этому результату Зу из V века!

Во втором томе Чжу Шицзе содержатся методы для вычисления площадей различных фигур и объёмов различных тел. Третий том содержит численные методы нахождения корней для систем полиномиальных уравнений высоких степеней. Через столетия на Западе эта процедура стала известна, как "схема Горнера", после того, как английский школьный учитель Уильям Горнер (1786-1837) опубликовал её в 1830-м году. Однако Горнера обвинили в плагиате этого приёма у лондонского часовщика Теофилиуса Холдреда, опубликовавшего его в 1820-м году. В любом случае, обоим им предшествовал не только Чжу Шицзе, но и итальянский первопроходец теории групп Паоло Руффини, развивший этот метод в XIX веке. ¹¹.

Следующие задачи взяты из второго и третьего томов работы Чжу Шицзе.

Задача 3-1.
Выразить объёмы следующих тел через a, b и h:

1. Усечённая пирамида высотой 12 сяку, нижнее основание которой является квадратом со стороной b = 6 сяку, а верхнее - квадратом со стороной a = 4 сяку.
2. Усечённый конус высотой h = 20 сяку, у которого длина окружности нижнего основания равна b = 72 сяку, а верхнего - a = 36 сяку. Считать π = 3. (решение)

Задача 3-2.
Сильная лошадь A пробегает 240 ри в день, а слабая лошадь B - 150 ри в день. Лошадь А стартует через 12 дней после B. Через сколько дней A догонит B? (решение)

Эта задача, с другими числами, появилась и в изданной в 1815 году традиционной японской книге Сампо: тэндзан синанроку, или Введение в алгебраические методы геометрии Сакабэ Ко:хана (1759-1824).

Задача 3-3a.
Решить следующие системы Рис.уравнений:

1. xy = 1024, где y/x + x/y = 4.25 и x>y;
2. xy = 4096, где x/y - y/x = 3.75.

Решения:

1. Перемножив исходные равенства, получим x² + y² = 4.25 xy = 4352. Но (x+y)² = 4352 + 2xy = 6400. Таким образом, x + y = 80 и xy = 1024. Два этих равенства значат, что x и y - корни квадратного уравнения t² - 80t + 1024 = (t-16)(t-64) = 0. Поскольку x>y, получаем x = 64, y = 16.
2. Аналогично, x² - y² = 3.75xy = 15360. Но x²y² = 16777216. Поскольку x²y² = x²[x² -(x² - y²)], имеем: x²(x² - 15360) = 16777216. Отсюда, x² - корень квадратного уравнения x⁴ - 15360x² - 16777216 = (x² + 1024) (x² - 16384) = 0, откуда x² = 16384, т.е. x = 128, y = 32.

Задача 3-3b.
Решить следующую систему уравнений относительно x>y>z:

(1) x² = y² + z² = 14384;
(2) x + y + z = 204;
(3) x - y = y - z. (решение)

Оригинальное решение Суансюэ Цымэня см. в конце этой главы.

4. Суанфа Тонь Зонь или "Системный трактат о математике", Чень Давэй, 1592 г.

Наверное, больше всего из китайских книг на японских математиков повлиял Трактат Чень Давэя, состоящий из 17 глав. В первой и второй он даёт основы вычислений и представляет соробан. Следующие 9 глав имеют те же заглавия, что и в оригинальных Девяти главах, хотя темы предметов и различаются, а четвёртая глава разделена на две. Оставшиеся главы состоят из более продвинутых задач. Книга Чень Давэя весьма практична, хотя есть в ней и несколько магических квадратов. Помимо инструкции по применению счётов, он рассматривает сплавы металлов и вычисление площадей различных фигур. В этом контексте он обсуждает различные приближения числа π, хотя приводимые им значения те же, что и в более ранней Суан-хсяо цымэнь. Для примера, мы приведём небольшое количество задач из этой книги Ченя. Особого внимания из них заслуживает задача 4-4, речь в которой идёт о применении "треугольника Паскаля". Этот знаменитый треугольник появлялся и в откомментированной версии оригинальных китайских "Девяти глав", изданных в 1261 году. Появлялся он и в более ранней работе Аль-Караджи (953-1029) из Багдада ¹², которая ещё будет обсуждаться. На Западе этот треугольник впервые появился в 1527 году, в "Космографии" Петруса Апиануса (1425-1552), хотя гораздо тщательнее, век спустя, его исследовал Блёз Паскаль (1623-1662). В Сети по треугольнику Паскаля можно найти массу информации. Его основное свойство заключается в том, что он состоит из биномиальных коэффициентов, полезных для возведения многочленов в степень, как например в задаче 4-4. Традиционные японские математики узнали об этом треугольнике из Суанфа Тонь Зонь.

Задача 4-1 (из главы 3 Суанфа Тонь Зонь, "Хо:дэн", или "квадратные поля").

Докажите следующие приблизительные факты:

1. Длина окружности с диаметром 1 примерно равна 3.
2. Диагональ квадрата со стороной 5 примерно равна 7.
3. Высота равностороннего треугольника со стороной 7 примерно равна 6.
4. Если площадь круга, вписанного в квадрат, равна 3/4 его площади, то π = 3.
5. Площадь квадрата, вписанного в круг, примерно равна 2/3 его площади.
6. Площадь круга, вписанного в равносторонний треугольник, примерно равна 4/7 его площади.
7. Площадь правильного 6-угольника, вписанного в круг, примерно равна 6/7 его площади.
8. Площадь круга, вписанного в правильный 6-угольник, примерно равна 6/7 его площади.
9. Площадь равностороннего треугольника, вписанного в круг, примерно равна 7/16 его площади.

Эти задачи о площадях приведены и в Дзинко:-ки Ёсиды 1627 года. (решение)

Задача 4-2 (последняя задача из главы 4 Суанфа Тонь Зонь, "Дзокуфу", или "Рис и деньги").

Мы произвели ткань весом 43 + 3/4 кин, состоящую из двух материалов, a и b, доли весов которых соотносятся как 4:1. Найти веса a и b. (решение)

Задача 4-3 (из главы 5 Суанфа Тонь Зонь, "О геометрических и арифметических последовательностях").

1. Мы хотим поделить 594 мон ¹³ между двумя людьми в пропорции 1:2. Сколько должен получить каждый из них?
2. Мы хотим поделить 672 серебряных рё между тремя людьми в пропорции 1:2:4. Сколько должен получить каждый из них?
3. Правительство хочет распределить 225.36 коку ¹⁴ риса между пятью классами домов. Каждый дом второго класса должен получить 0.8 от доли каждого из четырёх домов первого класса. Каждый дом третьего класса должен получить 0.8 от доли каждого из восьми домов второго класса. Каждый из домов четвёртого класса должен получить 0.8 от доли каждого из пятнадцати домов третьего класса. Каждый из 120 домов пятого класса должени получить 0.8 от доли каждого из 41 домов четвёртого класса. Сколько риса должен получить каждый дом и каждый класс в целом? (решение)

Задача 4-4 (из главы 6 Суанфа Тонь Зонь, "О треугольнике Паскаля").

Высчитать следующие степени многочленов с помощью треугольника Паскаля:

1. (a+b)³
2. (a+b)⁴,
3. (a+b)⁵.

Рис.2.9: "Треугольник Паскаля", изобретённый за сотни лет до Паскаля в Китае или Ираке, - мнемоническое приспособление для нахождения коэффициентов при раскрытии скобок в выражениях вида (a+b)ⁿ. Каждый его элемент находится, как сумма двух его соседних элементов сверху, а по краям расположены единицы. Таким образом, коэффициенты для (a+b)³ можно прочесть в его 3-й строке: a³ + 3a²b + 3b²a + b³. Его элементы равны биномиальным коэффициентам C_b^k = n!/[k!(n-k)!].

Задача 4-5.

1. Найти стороны x бу и x+15 бу прямоугольника площадью 1750 квадратных бу.
2. Найти стороны x бу и x+28 бу прямоугольника площадью 1920 квадратных бу. (решение)

Задача 4-6 (из главы 7 Суанфа Тонь Зонь, "О площадях полей").
Равносторонний треугольник ABC c центром G и стороной 14 разделили, как показано на диаг. 2.10, на 3 четырёхугольника равной площади. Найдите площадь ABC и длины сторон четырёхугольников. (решение)

Диаг. 2.10:Равносторонний треугольник со стороной 14 разделён на 3 равных 4-угольника. Найти площадь ABC и длины сторон 4-угольников.

Рис. 2.5: Сколько рулонов в этой куче? - из Дзинко:-ки, 1818. (Коллекция Фукагавы Хидэтоси)

Задача 4-7 (из главы 8 Суанфа Тонь Зонь, "Гражданский инженер").

1. Лошадь украли. Владелец, обнаружив кражу, пустился в погоню за вором, когда тот уже уехал на 37 ри. Проехав 145 ри, он узнал, что вор всё ещё опережает его на 23 ри. Сколько ещё ри ему надо проехать, чтобы догнать вора? (решение)
2. Несколько равных шаров выстроены так, как показано на диаг. 2.11: в основании 7 шаров, наверху - 2. Сколько всего шаров?
3. Много равных шаров выстроено, как показано на диаг. 2.12, в пирамиду, основание которой - равносторонний треугольник со стороной в 7 шаров. Сколько в ней всего шаров?
4. Равные шары выстроены в пирамиду, на сей раз - как показано на диаг. 2.13; её основание - квадрат со стороной в 12 шаров. Сколько в ней всего шаров?

Диаг. 2.11: Сколько всего кругов в этой трапеции?

Решение (2): Эту задачу можно решить и прямым пересчётом кругов. Однако знаменитая формула для суммы всех целых чисел от 1 до n 1+2+3+..+n = n(n+1)/2 даёт решение 3+..+7 = (1+..+7) - (1+..+2) = 7(7+1)/2 - 2(2+1)/2 = 25, которое легко обобщить на любое число кругов.

Диаг. 2.12: Сколько всего шаров в этой пирамиде?

Решение (3): Число шаров в слое p сверху равно 1+..+p = p(p+1)/2, т.е. в основании их 28. Отсюда легко получить общую формулу для числа шаров в пирамиде с основанием p: p(p+1)(p+2)/6, т.е. в данной пирамиде их 7(7+1)(7+2)/6 = 84.

Диаг. 2.13: Сколько всего шаров в этой пирамиде?

Решение (4): Число шаров в слое p сверху равно p².. Т.о. известная формула 1²+..+p² = n(n+1)(2n+1)/6 прямо даёт ответ 12(12+1)(2*12+1)/6 = 650.

Задача 4-8 (из главы 9 Суанфа Тонь Зонь, "Перевозки").

1. Служащие A и B работают в городской конторе. A приходит на работу каждый 12-й день, а B приходит на работу каждый 15-й день. Сегодня они встретились в конторе. Через сколько дней они встретятся в следующий раз? (решение)
2. Мальчик копит деньги следующим образом: в первый день он откладывает 1 мон, во второй - 2 мон, в третий - 2*2=4 мон, и т.д. Сколько всего он скопит за 30 дней?

Ответ на п.2: Сумма данной геометрической прогрессии равна 2³⁰-1 = 1073741823 мон. Эта задача приведена в издании Дзинко:-ки 1627 года.

Задача 4-9 (из главы 10 Суанфа Тонь Зонь, "Избыток и нехватка").

1. Есть N человек и большой отрез материи, длины G хики и постоянной ширины. Если каждый человек получит по 8 хики материи, то останется 15 хики, а если каждый получит по 9 хики, то останется 5 хики. Найти N и G.
2. N человек делят сумму денег в G рё. Если они разделятся на группы по трое, и каждая группа возьмёт для покупок по 5 рё, то останется 10 рё. Если же они разделятся на группы по пятеро, и каждая группа возьмёт для покупок по 9 рё, то ничего не останется. Найти N и G. ¹⁵ (решение)

Рис.2.6. Пункт 3 из задачи 4-11, приведённый в Суанфа тонь зонь

Задача 4-10 (из главы 11 Суанфа Тонь Зонь, "О линейных уравнениях").
Есть лимоны, груши, персики и гранаты. Два лимона и четыре груши стоят 4 бу. Четыре персика и семь гранатов стоят 3 бу. Восемь гранатов и один лимон стоят 2.4 бу. Найти стоимость каждого фрукта. (решение)

Задача 4-11 (из главы 12 Суанфа Тонь Зонь, "О теореме Пифагора").

1. Найти радиус окружности, вписанной в прямоугольный треугольник с катетами (решение)36 и 27 (см. рис. 2.14).
2. Найти сторону квадрата, вписанного в прямоугольный треугольник с катетами 12 и 6 (см. рис. 2.15).
3. Два стебля тростника равной высоты поднимаются над водой на 3 сяку. Если верхушку одного из них отклонить на 9 сяку в сторону берега, то она коснётся водной поверхности. Найти глубину дна (см. рис. 2.16). (решение)

Диаг. 2.14. Найти r.

Диаг. 2.15. Найти длину стороны квадрата.

Диаг. 2.16. Какова глубина дна?

3a + 2b + c = 39
2a + 3b + c = 34
a + 2b + 3c = 26.

1. Чень Давэй использовал значение π = 3, откуда напрямую следует ответ. Вписав в единичную окружность правильный 6-угольник, можно прямо увидеть, что его периметр равен 3.
2. Диагональ этого квадрата равна 5 √2 ≈ 7.07106.
3. По теореме Пифагора высота правильного треугольника равна h = √(7²-(7/2)²) ≈ 6.
4. Если сторона квадрата равна a, то πr² = (3/4)a². Но a=2r, откуда напрямую получаем π=3.
5. Если диаметр окружности равен 2r, то сторона квадрата равна 2r/√2, а его площадь 2r² = πr²*(2/3).
6. Площадь равностороннего треугольника равна 2ra/3, где a - сторона треугольника, а r - радиус вписанной окружности. Но a = 2r * tg(60^o) = 2√3*r, поэтому искомое отношение площадей равно 1/√3 ≈ 4/7.
7. Если радиус окружности равен r, то площадь вписанного в неё правильного 6-угольника в 6 раз больше площади правильного треугольника со стороной r, то есть равна S^' = 6*(1/2)r*(√3/2)r = (3√3/2)r². Деление на площадь круга S≈3r² даёт S^'/S≈√3/2≈6/7.
8. Стороны этих треугольников равны a, а высоты r=a/√3. Поэтому площадь 6-угольника S^'=6*(1/2)r*(2/√3)r = 2√3*r. Деление на S≈3r² опять даёт S/S^'≈√3/2≈6/7.
9. Площадь правильного треугольника со стороной a равна S^'=a*√3/4. Но a=r√3, поэтому S^'=(3√3/4)r². Деление на S≈3r² даёт S^'/S≈√3/4≈7/16.

Решение задачи 4-11.

1. Длина гипотенузы равна √(36²+27²)=45, но также (из чертежа) и 36-r+27-r, откуда r=(36+27-45)/2=9.
2. Если x - сторона квадрата, то из подобных треугольников 12/6=x/(6-x), откуда x=4.
3. Если x - глубина дна, то x²+9²=(x+3)², откуда x=12 сяку.

Рис.3.1: Иллюстрация из Дзинко:-ки издания 1715 года, сопровождающая задачу о плодящихся мышах. В данной главе это задача 4. (Из коллекции Фукагавы Хидэтоси)

Глава 3. Японская математика и математики эпохи Эдо

С младых лет я посвятил много времени изучению математики и прочёл много книг. Я навещал своего учителя, живущего далеко отсюда, и упорно учился. Но вот, теперь дети забавляются фокусами и пишут плохие стихи. Плачевно, что они тратят столь много времени впустую. Если они читают и пишут лишь стихи, то пусть уж лучше эти стихи будут математическими. Я запишу формулы Дзю:гай-року в форме стихов. - Из предисловия к книге Имамуры Томоаки 1640 года Инки санка, или "Стихи об умножении и делении" для детей.

В главе 1 мы вкратце рассмотрели исток традиционной японской математики васан, с появления счётов в Японии и публикации в 1627 году Дзинко:-ки Ёсиды Мицуёси, и то, как на форму эволюции васан сильно повлияла изоляционистская политика клана Токугава с начала XVII века. Попутно мы упоминали нескольких самураев, которые, получив лицензию от своих Учителей Математики, могли учить в дзюку или же открывать свои собственные частные школы на дому или рядом с домом. Теперь мы опишем несколько важнейших математических работ эпохи Эдо и их создателей, самураев-математиков. Как и в предыдущей главе, мы попытаемся передать их вкус через содержащиеся в них задачи, которые в основном должны быть доступны для учащихся высшей школы.

Васан в XVII веке

Есида Мицуёси и Дзинко:-ки

Рис.3.2: Уличная сцена из Дзинко:-ки, иллюстрирующая выгоды от обучения соробану в торговле. Взято из издания, опубликованного между 1818 и 1829 г. (Коллекция Фукагавы Хидэтоси)

Немногое можно добавить к биографии первого идентифицируемого японского математика, Мо:ри Сигэёси, написавшего в 1622 году брошюру о применении соробана. Известно лишь, что у него было три ученика: Имамура Томоаки (?-1668), Такахара Ёситанэ и Ёсида Мицуёси (1598-1672), последний из которых и опубликовал Дзинко:-ки, ответственную за многое из воспоследовавшего далее.

Про Ёсиду мы знаем чуть больше. Родившийся в Киото в 1598 году, он был внуком купца Суминокура Рё:и (1554-1614), нажившего миллионное состояние на торговле с Китаем и другими странами Восточной Азии, поэтому Ёсида мог иметь лёгкий доступ к китайским математическим текстам. У Мо:ри он научился арифметике, а у интеллектуала Суминокура Соан - математике из Суанфа тонь зонь Чень Давэя. Впоследствии Ёсида потерял зрение, несомненно - из-за множества пересмотров Дзинко:-ки; умер он в 75 лет.

Большинство примеров в выдержавшей более 300 изданий Дзинко:-ки касаются вычислений, полезных для повседневной жизни и ведения бизнеса. Тут мы приводим горсть задач из издания 1643 года, опубликованного при жизни Ёсиды. Из содержащихся в нём 270 задач 36 - примеры применения соробана, 28 - про обменные курсы, 35 - про измерение площадей полей. Почти все они взяты из китайских текстов.

Задача 1. Эта задача цитируется и в китайской Цзючжань Суаншу.

Есть поле в форме кольца. Длина его внешней окружности равна 120 кэн 1, а внутренней - 84 кэн. В середине поля находится дом, поэтому его диаметр нам не измерить, но известно, что расстояние между этими окружностями равно 6 кэн. Найти площадь поля без помощи числа π.

Оригинальный ответ: S = (120+84)/2 * 6 = 612 цубо.

	Рис.3.3: Разносчик масла должен отмерить неудобный объём масла с помощью лишь двух ковшей. Из издания Дзинко:-ки 1643 года (Коллекция Фукагавы Хидэтоси).

Задача 2. Эта задача, нусубито-сан ("исчисление воров") была взята из Сунцу Суанцзинь (см. гл.2, задачу 2-2).

Ночью воры украли из сарая рулон материи. Когда они делили добычу под мостом, прохожий услышал их разговор: "Если каждый из нас получит по 7 тан, то останется 8 тан, но если каждый захочет взять по 8, то 7 тан не хватит". ² Сколько там было воров, и сколько ткани они украли?

Задача 3. В эпоху Эдо люди использовали для освещения домов сурепковое масло (аналогичное рапсовому). Отсюда - задача абура-вакэ ("распределение масла"):

Разносчик сурепкового масла торговал маслом. Однажды вечером, по пути домой, покупатель спросил у него 5 сё: масла.³ Но у разносчика оставалось в большой кадке лишь 10 сё:, и он не мог отмерить масло иначе, кроме как с помощью двух пустых ковшей ёмкостью 3 и 7 сё:. Как же разносчик отмерил 5 сё: покупателю?

Оригинальное решение: Пусть большая кадка - это A, ковш в 3 сё: - B, а ковш в 7 сё: - C. Зачерпнём в В трижды из A, переливая в C. Тогда в A останется 1 сё:, в C будет 7 сё:, а в B останется 2 сё:.
Далее, выльем всё из C в A. Тогда в A окажется 8 сё:. Теперь выльем все 2 сё: из B в C. Наконец, добавим с помощью B 3 сё: из A в C. Тогда в C окажется 5 сё:, которые разносчик и продаст покупателю.

Возможно, эту задачу придумал сам Ёсида; по крайней мере, ни в каких китайских источниках её нет. Она аналогична задаче, известной на Западе, как "задача о трёх кувшинах". ⁴

Задача 4. Эту задачу нэдзуми-сан ("исчисление мышей") Ёсида даёт, как пример для соробана. Очевидно, что она аналогична задаче 4-8 из предыдущей главы.

1 января в доме завелась пара мышей, родившая 6 мышонков 6 мышек. Таким образом, в конце января в доме было уже 17 мышей: 7 самцов и 7 самок.
1 февраля каждая из 7 пар родила 6 мышонков и 6 мышек, поэтому к концу февраля в доме было 98 мышей, разбившихся на 49 пар. И далее, каждая пара мышей рожала по 6 пар каждый месяц.

1. Найдите число мышей в доме к концу декабря.
2. Пусть длина каждой мышки 4 сун (12 см). Какова будет длина всех мышей, если все они выстроятся в ряд так, что каждая мышь будет держать зубами кончик хвоста следующей?

Оригинальный ответ: (1) 27 682 574 402.
В книге написано число мышей к концу каждого месяца: 2*7=14, 2*7*7=98, 2*7³=686, 2*7⁴=4802, 2*7⁵=33614, 2*7⁶=235298, 2*7⁷=1647086, 2*7⁸=11529602, 2*7⁹=80707214, 2*7¹⁰=564950498, 2*7¹¹=3954653486, 2*7¹²=27682574402.
(2) Общая длина мышей равна 2*7¹²*12 см. В Дзинко:-ки говорится: "эта длина равна длине [пути] вокруг Китая и Японии. Фактически, она в 7 раз больше расстояния от Земли до Луны". На самом деле, последняя оценка недалека от истинной. ^7'

Имамура Томоаки (?-1668)

Дзинко:-ки пробудила большой интерес к задачам, с которыми можно справиться вычислением, включая вычисление площадей многоугольников, объёмы тел и, в частности, вычисление числа π. Одним из математиков, писавших на эти темы, был Имамура Томоаки ⁵ из Осаки. Вот всё, что о нём известно: он был одним из "трёх почётных учеников" Мо:ри Сигэёси; в 1639 году он опубликовал работу Дзю:гайроку, название которой он, видимо, взял из старой китайской книги по географии, Сэнгайкё:. В следующем году он опубликовал её версию, отредактированную для детей, Инки санка ("Стихи об умножении и делении"). В начале этой главы мы цитировали предисловие Имамуры к этой книге. Он говорит: "Если ребёнок прочтёт стих из этой книги и попытается проделать вычисление на соробане, этот опыт в будущем ему пригодится. Если же какой-нибудь ребёнок захочет узнать доказательства формул, пусть смотрит мою книгу Дзю:гайроку".

В Дзю:гайроку Имамура определил, что квадратный корень из 152.2756 равен 12.34; вычислил кубический корень из 1880, площади правильных 3,5,6,7,8,9 и 10-угольников, и доказал много формул для объёмов различных тел. Вот задача из "стихов о площадях правильных многоугольников" из Инки санка.

Задача 5.

1. Сторона правильного n-угольника равна s. Покажите, что его площадь:
   • (a) при n=3 равна 0.433s²;
   • (b) при n=5 равна 1.73s²;
   • (c) при n=7 равна 3.64s²;
   • (d) при n=8 равна 4.828s²;
   • (e) при n=9 равна 6.093s².
2. Почему формулы для n=4 и n=6 пропущены?
3. Покажите, что объём собагара (гречишного зерна), имеющего форму тетраэдра (с ребром s), примерно равен 0.11783s³. (решение)

	Рис.3.4. Как и многие другие математики, Мурамацу Сигэкиё приближал π, вписывая правильные n-угольники в единичную окружность. Тут показан 8-угольник, однако Мурамацу рассматривал и 32768-угольник, вычислив π до 22-го знака, лишь 8 из которых были верными.

Мурамацу Сигэкиё (1608-1695)

Хотя у китайцев ещё с VI века и было значение числа π точнее, чем 3.14, по некоторым причинам в начале эпохи Эдо японские математики использовали значение π=3.16. Это значение можно найти в учебнике Мо:ри Сигэёси 1622 года Варидзансё, в первом издании Дзинко:-ки и в Инки санка Имамуры. Никто не знает, почему так произошло. Во многих традиционных задачах окружности определяются своим диаметром, а не радиусом, и поэтому их площадь считается не по формуле S=πr², а как S=(π/4)d². Поскольку 3.16=4*0.79, возможно, было удобно округлять π для записи S=0.79*d², однако это лишь предположение.

В эту "эпоху π=3.16" Мурамацу Сигэкиё показал, что периметр правильного 2¹⁵=32768-угольника, вписанного в единичную окружность, равен 3.141592648. На самом деле, в своей книге Сансо ("Математический склад") 1663 года он привёл 22 цифры, однако правильными были лишь 8. Далее мы приводим из этой книги таблицу периметров P_n правильных 2ⁿ-угольников, вписанных в единичную окружность. С помощью формулы P_n=2ⁿ*sin(π/2ⁿ) и калькулятора читатели могут убедиться в правильности первых 8 знаков.

• P₃=3.061467458 ; P₄=3.121445152 ;
• P₅=3.136548490 ; P₆=3.140331156;
• P₇=3.141272509 ; P₈=3.141513801 ;
• P₉=3.141572940 ; P₁₀=3.141587725;
• P₁₁=3.141591421 ; P₁₂=3.141592345 ;
• P₁₃=3.141592576 ; P₁₄=3.141592634;
• P₁₅=3.141592648.

Исомура Ёсинори (1630-1710)

Как и другие математики той эпохи, включая Имамуру, Исомура Ёсинори изучал задачи, имеющие приближённые решения. Исомура был самураем клана Нихонмацу в префектуре Фукусима. В 1661 году он опубликовал Санпо: Кэцу Гисё: ("Глубины математики"), в которых использовал значение π=3.16. Однако в 1684 году он издал вторую, аннотированную версию, Тосё Санпо: Кэцу Гисё:. В ней, подстёгнутый Дзинко:-ки и Мурамацу, Исомура с помощью 2¹⁷=131072-угольника вычислил π=3.141592653, подтвердив и уточнив результат своего предшественника.

Исомура, также, развил подход к вычислению объёмов простых тел нарезанием их на диски и сложением объёмов этих дисков. Это давало приближённый результат, но [интегральное] исчисление тогда ещё только изобреталось на Западе и не существовало в Японии, поэтому никто и не мог бы ждать чего-то большего. Вот задача из первого издания.

Задача 6.

1. Найти объём правильного тетраэдра с ребром длины 1.
2. В правильном треугольнике со стороной 1 вершины соединили с центром, и в получившиеся 3 треугольника вписали окружности. Показать, что диаметр этих окружностей 2r ≅ 0.26794. (решение)
3. В правильном 5-угольнике со стороной 1 вершины соединили с центром, и в получившиеся 5 треугольников вписали окружности. Показать, что их диаметр равен 2r ≅ 0.50952.

Вот оригинальное решение части (1). Рассмотрим куб со стороной 1/√2. Вырежем из него 4 пирамиды так, чтобы остался тетраэдр с ребром длины 1. Поскольку объём куба равен (1/√2)³, а объём каждой из этих пирамид равен (1/√2)³/6, объём тетраэдра равен (1/√2)³ - 4 * (1/√2)³/6 = √2/12.

Сэки Такакадзу (1640?-1708)

	Рис.3.5. Портрет величайшего японского математика Сэки Такакадзу, из рукописи Косэцуки, или "Предки математиков" (библиотека Цурумаи).

Уровень васан испытал резкий скачок в конце XVII века, в основном - благодаря работам Сэки Такакадзу, самого известного математика Японии. О силе Сэки рассказываетс множество историй, однако, как и к историям про юного Гаусса, к ним стоит относиться с скептицизмом. Большинство работ Сэки было опубликовано посмертно его учениками, и поскольку математики в Японии традиционно проявляли уважение к своим учителям, всегда трудно в точности узнать, что сделал он, а что - не он. Точные дата и место рождения Сэки неизвестны, но он был близким современником Ньютона. Происходя из самураев, он был в детстве принят в благородную семью Сэки Городзаэмона, и далее действовал под этой фамилией. Впоследствии он работал с казной клана Ко:фу, главой которого был лорд Токугава Цунасигэ. В 1704 году Сэки был взят на работу, как самурай сёгуната, в правительство Токугава, и работал два года казначеем среднего уровня. В 1706 году он вышел в отставку, а в 1708 - умер.

Сэки возмужал в подходящий момент, как раз в эру Гэнроку, и у него была возможность изучить обильное количество математических книг, которые тогда издавались. В 1672 году, когда ему было около 30 лет, он написал рукопись "Решения нерешённых задач из Санпо: кэцу гисё:" Исомуры. Через 2 года он опубликовал Хацуби санпо: ("Математика в деталях"), состоявшую из решения 15 нерешённых задач из книги Савагучи Кадзуюки 1671 года Кокон санпо:ки ("Старая и новая математика").

На самом деле, из книг Сэки при его жизни была опубликована лишь Хацуби санпо:. Умирая, он оставил 21 книгу в рукописях, включая 7 по астрономии. В 1712 году его ученик Араки Мурахидэ опубликовал 4 тома работ Сэки под заглавием Кацуё: санпо: ("Коллекция важных математических результатов"). Именно из этой коллекции и известно о многих достижениях Сэки.

Хотя иногда и появляются сомнения в ассоциации имени Сэки с изобретением энри (определённого интеграла), несомненно, что именно он первым разработал теорию определителей, за десятилетие до Лейбница. Он, также, открыл числа Бернулли до Якоба Бернулли, и схему Горнера за 150 лет до Горнера, хотя в последней ему и предшествовали китайцы. Тут мы для начала представим задачу Кайфуку дай-но хо: ("Определители"), датирующуюся 1683 годом (на самом деле, для понимания решения не надо знать, что такое "определитель").

	Рис.3.6. Оригинальные обозначения Сэки для определителей из его рукописи 1633 года Кайфуку дай (Японская Академия).

Задача 7.

1. Из уравнений на переменную y

   ay + b = 0,
   cy + d = 0,
   

   где коэффициенты a,b,c,d - ненулевые константы или функции от другой переменной x, исключить y и найти соотношение на a,b,c и d.


2. Из уравнений на переменную y

   ay2 + by + c = 0, (3.1)
   dy2 + ey + f = 0, (3.2)
   gy2 + hy + i = 0, (3.3)
   

   где все коэффициенты опять функции от x, найти соотношение на a,b,c,d,e,f,g,h и i.

Решения. (1) Легко увидеть, что y = -b/a = -d/c, откуда ad-bc=0.

(2) (3.2)*a - (3.1)*d даёт y = (af-dc)/(bd-ae). Аналогично, (3.3)*d - (3.2)*g даёт y = (di-fg)/(eg-dh). Отсюда (af-dc)(eg-dh) = (bd-ae)(di-fg), т.е. aei+bfg+cdh-afh-bdi-ceg=0.

Сэки изобразил эти соотношения в виде диаграмм (см.рис.), известных читателям, которые знакомы с линейной алгеброй.

	Рис.3.7. Один из подлинных чертежей Сэки для 15-угольника из его книги Кацуё: санпо: (Мацудзаки Тосио).

Как и его современники, Сэки был глубоко заинтересован в вычислении числа π, однако в отличие от других он разработал для этого оригинальный метод. Следуя методу Мурамацу, он высчитал периметры 2¹⁵-угольника, 2¹⁶-угольника и 2¹⁷-угольника: P₁₅ = 3.14159264, P₁₆ = 3.14159265 и P₁₇ = 3.141592653. Далее он неожиданно заявил: π = P_∞ = P₁₆ + (P₁₆−P₁₅)(P₁₇−P₁₆) / [(P₁₆−P₁₅) − (P₁₇−P₁₆)] = 3.14159265359.

То есть, π равно периметру правильного многоугольника с бесконечным числом сторон, вписанного в единичную окружность, и он записал свой результат в терминах P₁₅, P₁₆ и P₁₇. Более того, в этой оценке на две точные цифры больше, чем в правильных 10 цифрах из P₁₇. Сэки не раскрыл ход своей мысли, но мы можем его реконструировать. Пусть a=a₁ = P₁₆-P₁₅, и a₂ = P₁₇-P₁₆. В задаче 4-8 главы 2 мы обсуждали геометрический ряд a+ar+ar²+ar³+.... Его сумма равна a/(1-r). Пусть r=a₂/a₁Тогда, если предположить, что π можно приблизить суммой геометрической прогрессии ^8', то P_∞ = P₁₅ + a/(1-r) = P₁₆ + a₁a₂/(a₁-a₂) - результат Сэки.

Эта полученная Сэки новая оценка π была опубликована его учеником Такэбэ Катахиро в Тэцудзюцу Санкэй, где Сэки сначала показал, что π ≅ 355/113. Об этой оценке Такэбэ написал: "В стародавние времена мой учитель Сэки Такакадзу нашёл оценку π ≅ 355/113 с помощью своего собственного метода. Через 20 лет он узнал, что точно такая же оценка, π ≅ 355/113, была получена Зу Чоньжи (гл.2) в его Зуйси ("Записи эпохи Зуй", 581-619). Удивительно, как два выдающихся математика нашли одно и то же значение в разных странах и в разные века."

Задача 8. Как мы уже говорили, из-за вычислений π Сэки интересовался свойствами правильных n-угольников. Например, в работе Каку хо: ("Углы правильных многоугольников"), том 3 Кацуё: санпо:, он вычисляет радиусы вписанных и описанных окружностей для n-угольников при n=3..20. Эти вычисления он делает с помощью сложных чертежей (см. рис.3.7), без тригонометрических функций, однако мы можем дать понятие об этих результатах через следующие примеры:

1. Найти для правильного треугольника со стороной 1 уравнение, связывающее радиусы r₃ и R₃ его вписанной и описанной окружностей.
2. Сделать это же для квадрата со стороной 1, и
3. для 5-угольника со стороной 1. (решение)

Рис.3.8. В книге Фуки Дзинко:-ки ("Сокровища Дзинко:-ки") 1778 года анонимный автор предлагает взвесить слона, посадив его в лодку и пометив уровень осадки, а затем заменяя его на камни известного веса, пока осадка не достигнет уровня, помеченного при загрузке слона. (Коллекция Фукагавы Хидэтоси)

Васан в XVIII веке

Такэбэ Катахиро (1664-1739)

Через несколько десятилетий после того, как Ньютон и Лейбниц развили интегральное исчисление на Западе, японские математики тоже стали предпринимать шаги в этом направлении, хотя они и не разработали зрелой теории. Человек, от которого мы больше всего знаем об этих начальных усилиях - и, наверное, сам крупнейший из авторов этих усилий, - это самый известный из учеников Сэки, Такэбэ Катахиро ⁶, которого мы недавно упоминали. Такэбэ стал учеником Сэки в 13 лет, а в 19 уже опубликовал свою первую книгу, Кэнки санпо: ("Глубокое изучение математики"). Впоследствии он стал самураем сёгуната, заняв такую же позицию, как и его учитель. В 1719 году правительство поручило Такэбэ создать карту Японии, которая стала известной за свою детальность; однако, до наших дней она не сохранилась. И хотя, как уже упоминалось, Сэки иногда приписывают изобретение энри, многие чётки свидетельства указывают, что фактически это сделал Такэбэ.

За свою жизнь Такэбэ опубликовал 3 книги, а ещё 12 его работ остались в рукописях. Первая из этих рукописей - Тайсэй санкэй ("Полная книга по математише") 1710 года в 20 томах. Другая - Тэцудзюцу санкэй ("Ряды") 1722 года.

С помощью правильного 1024-угольника, вписанного в окружность, Такэбэ даёт в Тайсэй санкэй приближение π = 5419351/1725033 = 3.141592653589815383241944, отличающееся от реального π на 0.000000000000022144779300; это показывает, что вычисления Такэбэ были экстраординарно аккуратны.

В Тэцудзюцу санкэй Такэбэ вычислил π = 3.14159265358979323846264338327950288419712. Из этих 42 знаков 41 верный. Метод Такэбэ весьма сложен: он использует бесконечные ряды, которых не было в китайской математике, и которые он изобрёл сам. Детали см. в главе 9.

Мацунага Ёсисукэ (1692?-1744)

Как только для π появилась замкнутая формула - например, π/4 = arctg(1/2) + arctg(1/3) (на Западе это произошло в начале XVIII века), единственным ограничением для вычисления всё большего числа цифр π стала простая скука. Однако японцы не использовали тригонометрических функций, и таких формул у них не было, хотя и были ряды. В любом случае, в XVII-XVIII веках ещё не было понятно, что π иррационально, поэтому, возможно, японские и западные математики мечтали найти место, начиная с которого десятичные знаки π начнут повторяться.

Одним из охотников за цифрами π был Мацунага Ёсисукэ. Известно о нём мало. Мацунага был самураем клана Иваки, глава которого, Найто: Масаки (1703-1766) тоже был математиком. Мацунага написал 42 рукописи, главная из которых - Хо:эн санкэй ("Математика кругов и квадратов") 1739 года. В ней он правильно вычислил 50 знаков π. В неопубликованной рукописи Хо:эн дзассан ("Эссе о математике кругов и квадратов") он правильно вычислил 52 знака π - рекордное по точности значение из найденных в рамках васан. Вот задача про π, дающая представление о методах Мацунаги.

Задача 9. Пусть 3.1415926 < π < 3.1415927. Покажите, что тогда верно приближение Сэки π=355/113. (решение)

Мацунага ввёл в оборот множество численных методов для соробана, другими словами - "компьютерных программ". Некоторые из них относятся к энри, и мы обсудим их в главе 9.

Наканэ Гэндзюн (1701-1761)

Как и на Западе, математики в Японии, такие как сэки и Исомура, проявляли интерес к таким "recreation pursuit", как магические квадраты и круги. Несомненно, что в этом они ушли гораздо дальше своих коллег с Запада, составляя квадраты 20x20, не говоря уже о магических квадратах и эллипсах. Одним из математиков, работавших в этой области, был Наканэ Гэнкэй (1662-1733), выучившийся у Такэбэ. В возрасте 60 лет, в 1721 году, Гэнкэй, считавшийся одним из самых учёных людей Японии, получил от Токугавы Ёсимунэ предложение перевести две китайские книги по астрономии. Через десятилетие он сделал большое количество наблюдений за солнцем и луной, и посвятил свою книгу, в рукописи, Токугаве Ёсимунэ. Наканэ Гэндзюн изучал математику со своим отцом в Киото, и далее в Эдо с Такэбэ. Главная работа Гэндзюна - книга Кания отоги дзо:си ("Сборник интересных математических результатов"), опубликованная в 1743 году. Эта книга содержит 69 задач, из которых мы приведём две развлекательные: "Разрезание бумаги" и "Магические квадраты".

Задача 10.

1. Согнуть и разрезать (по сгибам) прямоугольный лист бумаги размером 1×2 так, чтобы из получившихся кусков можно было составить квадрат со стороной √2
2. Согнуть и разрезать прямоугольный лист бумаги размером 1×3 так, чтобы из получившихся кусков можно было составить квадрат со стороной √3
3. Для каждого из случаев, показанных на чертеже 3.7, согнуть и разрезать лист бумаги, составленный из пяти единичных квадратов так, чтобы из получившихся кусков можно было составить квадрат со стороной √5. (решение)

Рис.3.9. Чертежи разрезания бумаги из книги Наканэ Гэндзюна 1743 года Кания отоги дзо:си (Масудзаки Тосио).

Задача 11.

1. Используя по 3 раза числа 1,2 и 3, составить магический квадрат: такой, что сумма чисел в каждом его столбце, в каждой строке и по каждой диагонали равна 6.
2. Используя по 4 раза числа 1,2,3 и 4, составить магический квадрат: такой, что сумма чисел в каждом его столбце, в каждой строке и по каждой диагонали равна 10.

Адзима Наонобу (1732-1798)

Весь XVIII век японские математики придумывали геометрические задачи, приводящие к уравнениям высших степеней. Самая известная из них - "Задача храма Гион", которая состояла из уравнения 1024-й степени (формулировку см. в гл.7). Аналитического (т.е., точного) решения для неё так и не было найдено, но, как уже говорилось в главе 1, Адзима Наонобу стал известен тем, что свёл её от уравнения 1024-й степени к уравнению 10-й степени. Свои вычисления он оставил в неопубликованной рукописи 1774 года Кио:то Гион дайто: дзюцу ("Решение задачи храма Гион").

Задача храма Гион - это лишь один из множества вкладов Адзимы в различные ветви математики, и хотя при жизни он ничего не опубликовал, он считается величайшим японским математиком XVIII века. Адзима родился в 1732 году в ветви Эдо клана Синдзё:, и в 23 года стал самураем ⁷. В 42 он атаковал задачу храма Гийон, в 43 получил должность гун бугё:, а в 1798 году умер в Эдо.

Помимо официальной работы, Адзима изучал математику в школе Сэки в Эдо, в которой он получил лицензию Учителя Математики. Работы Адзимы отмечены оригинальностью, и про него говорят, что если бы он жил на Западе, то наверное был бы равен Джозефу Лагранжу - возможно, величайшему математическому физику после Ньютона. 42 книги, которые остались после него в рукописях, впоследствии широко разошлись в рукописных копиях. Адзима ближе всех японских математиков подошёл к созданию полной теории интегрирования. Через год после смерти Адзимы один из его студентов, Кусака Макото (1764-1839), подготовил к публикации (но так и не опубликовал) коллекцию работ Адзимы, Фукю: санпо: ("математические шедевры"), содержащую "Задачу Мальфатти", написанную за 30 лет до итальянца Гиана Франческо Мальфатти (см. главу 8).

В ходе решения сложной задачи в Фукю: санпо: Адзиме понадобилось найти значение 10ⁿ при 0 < n < 1. Он пишет: "Я получил новый метод для нахождения 10ⁿ при 0 < n < 1, что является сложной задачей". Это обеспечило базу для примера, который мы тут приводим, демонстрирующего метод Адзимы. ⁸

Задача 12. Решая уравнение x¹⁰-10=0, Адзима показал, что 10^0.1=1.258925. Далее он показал, что уравнение x¹⁰-10^0.1 = x¹⁰-1.258925 = 0 имеет корень 10^0.01=1.023293. Исходя из этого,

1. С помощью значения 10^0.1=1.258925 найти значение 10ⁿ для n=0.9, 0.8, ..., 0.2 с точностью в 7 знаков.
2. С помощью значения 10^0.01=1.023293 найти значение 10ⁿ для n=0.09, 0.08, ..., 0.02 с точностью в 7 знаков.
3. Исходя из пп. 1 и 2, найти 10^2.56 с точностью в 7 знаков. (решение)

Фудзита Садаскэ (1734-1807) и Фудзита Кагэн (1772-1828)

Основная часть этой книги посвящена задачам сангаку, но эта коллекция не была бы возможна без работы наших уважаемых предшественников Фудзит, вскользь упомянутых в главе 1. Старший из них, Садаскэ, родился в 1734 году в провинции Сайтама и учился в школе Сэки. В 1762 году правительство Токугава назначило его помощником астронома, но из-за проблем со зрением (следствие математического азарта) через 5 лет он вышел в отставку. В 1768 году он стал официальным математиком клана Курумэ, глава которого Арима Ёриюки (1714-1783) тоже был знаменитым математиком. В 1769 году Арима опубликовал Сюки санпо: ("Драгоценные камни математики"). Около 1780 года Фудзита стал четвёртым наследником Сэки, т.е. главой школы Сэки.

Более всего Садаскэ знаменит своей книгой 1781 года Сэйё: санпо: ("Математика в деталях"), но он также помог своему сыну Кагэну опубликовать первую коллекцию задач сангаку - Синпэки санпо: ("Священная математика"), появившуюся на свет в 1789 году. В главе 4 мы поговорим об этой книге подробнее, и следуя почтенной традиции, приведём из неё множество примеров. В 1807 году Кагэн, работавший, как и его отец, в клане Карумэ, опубликовал второе издание этой книги, Дзоку синпэки санпо:.

Вот задача из более ранней Сэйё: санпо: Садаскэ.

Задача 13.

1. Касающиеся окружности с радиусами a и b касаются прямой l в точках D и E. Показать, что DE = 2√ab.
2. Натуральные числа (p,q,r) образуют пифагорову тройку, если p²+q²=r², то есть, если они являются длинами сторон прямоугольного треугольника. Эта тройка называется "примитивной", если у неё нет общих делителей кроме 1. Показать, что (p,q,r) - примитивная пифагорова тройка, если
   p=2mn, q=m²-n², r=m²+n²
   для любых взаимно простых m>n>0 разной чётности.
3. Найти все 5 пифагоровых троек для r≤41.

Решения:

1. Опустим перпендикуляры AD и BE из центров окружностей на l, и AC - из A на BE. Тогда, по теореме Пифагора, (a+b)² = (b-a)² + DE², откуда DE = 2√ab. (Этот результат пригодится для многих следующих задач.)
2. Пусть в предыдущей задаче мы хотим, чтобы DE=AC было целым. Поскольку DE

   = 2√ab, для этого достаточно условий √a=n, √b=m, где m и n - целые. Но тогда p=AC=2mn, q=BC=m²-n², r=AB=m²+n², т.е. треугольник ABC - пифагоров. Условие на примитивность предлагается доказать самостоятельно. ⁹

3. В Сэйё: санпо: Садаскэ приводит все примитивные пифагоровы тройки для r < 1000. Для r < 45 их список таков: (3,4,5), (5,12,13), (8,15,17), (7,24,25), (12,35,37), (20,21,29) и (9,40,41).

В васан ^9' это был простейший метод нахождения примитивных пифагоровых троек.

Васан в XIX веке

Айда Ясуаки (1747-1817)

Появлению многих сангаку мы обязаны ученикам и последователям геометра Айда Ясуаки ¹⁰, уроженца провинции Ямагата на северо-востоке Японии. Родившийся в 1747 году, в 16 лет Айда поступил в местную школу Окадзаки для изучения математики. В 23 года он подался в Эдо, работал как самурай в дорожной бригаде по сооружению дорог и набору рабочих. Кажется, только этим он и занимался, ничего не делая в математике, пока в возрасте 35 лет он не вывесил сангаку в храме Атаго. Один из членов дорожной бригады оказался студентом Фудзиты Садаскэ и привёл его познакомиться со своим учителем, на тот момент - главой школы Сэки. В дружественной манере Фудзита посоветовал Айде исправить ошибку в табличке, которую тот вывесил.

Однако Айда обиделся на тёплый совет Фудзиты и организовал Сайё: рю: ("Наилучшую Математическую Школу"), встав в оппозицию к Сэки рю: ("Школе Сэки"). В результате возникла затяжная клановая вражда, но математические способности Айды были несомненны. Более того, охваченный лёгким математическим безумием, он написал около 1300 книг, 12 из которых были опубликованы. "Книги", возможно, тут слишком растянутое понятие: неопубликованные 1289 состояли примерно из 20 страниц каждая.

Айда достиг высокого мастерства в геометрии. Его Санпо: Тэнсё:хо: ("Алгебраическая геометрия"), состоящая из 195 томов, является несомненно крупнейшим учебником математики в истории, а его Санпо: канту: дзюцу ("Общие методы в геометрии") состоит из 65 томов. Возможно, главным вкладом Айды было то, что его Наилучшая Математическая Школа подготовила множество математиков на северо-востоке Японии, в результате чего многие сангаку этой части страны дожили до наших дней. Поскольку в данной книге читатель встретится со множеством задач школы Айды (например, гл.4, задача 37 и гл.5, задача 21), тут мы их не приводим.

Другие математики конца эпохи Эдо

Японских математиков, внёсших вклад в развитие васан слишком много, чтобы приводить имена их всех. Один из важнейших для данной книги - Ямагути Кандзан, являющийся чем-то чуть большим, нежели тень. Родился он в Суибара, префектура Ниигата, около 1781 года; изучал математику в Эдо, и умер в 1850 году. Его основное наследство - объёмистый путевой дневник, результат шести пеших турне по Японии, которые он предпринял, чтобы записывать задачи сангаку. Помимо двух, все описанные им таблички были утрачены. Глава 7 данной книги составлена из обширных выдержек из этого дневника, включая задачи.

Сравнимую важность имеет для нас и Ёсида Тамэюки (1819-1892), самурай клана Овари из Нагои. Ёсида вёл свои исследования со многими учителями и оставил множество рукописей, содержащих решения задач храмовой геометрии. Его решения ценны своей простотой, ясностью и красотой, и некоторые из них мы представим в данной книге. Один из её авторов, Фукагава Хидэтоси, пытался найти место, где стоял дом Ёсиды в Нагое, но втуне.

Весьма важной фигурой был и Учида Кё: (1805-1882), математический вундеркинд, попавший в школу последователей Сэки в 11 лет и получивший лицензию учителя в 18. Он знал голландский, и когда он открыл свою собственную школу, то назвал её "Математика". Работы Учиды накрывают многие области: не только математику, но и астрономию, географию, кадастр. Он стал известным учителем, ученики приезжали к нему со всей Японии. В 1879 году он стал членом Токийской Академии при новом правительстве Мэйдзи. одна из его главных работ, Кокон санкан ("Математика в настоящем и прошлом") 1832 года примечательна тем, что содержит знаменитую Теорему Содди о [hexlet] 1937 года: в виде задачи сангаку она появилась в 1822 году (см. гл.6, задача 16).

Развитие энри продолжили другие математики XIX, включая Ваду Ясуси (1787-1840) и Учиду Кю:мэй (?-1868), но поскольку их работы в основном касались интегрирования, упоминать их мы будем лишь в главе 9. Данную же главу мы завершим элементарной задачей Чибы Танэхидэ (1775-1849), родившегося в деревне, но впоследствии изучавшего математику в школе Хасэгавы Хиросэ в Эдо. В 53 года Чиба стал самураем клана Ичиносэки в провинции Иватэ. Когда, в 1830-м году, появилась на свет его книга Санпо: синсё ("Новая математика"), она стала одной из самых популярных математических книг в Японии. Она содержит описание почти всей традиционной японской математики, включая энри и нижеследующую задачу, решение которой будет крайне полезно для всего дальнейшего.

С помощью чертежа 3.11 докажите Теорему Пифагора для треугольника ABC.

Чертёж 3.11: докажите Теорему Пифагора.

(2): Тут мы применим формулу четверного угла: sin(4θ)=cosθ*(4sinθ-8sin³θ). Аналогичная процедура даст 2R₄²-1=0 и 2r₄-1=0. 10'

(3): Тут соответствующая формула такова: sin(5θ)=16sin⁵θ-20sin³θ+5sinθ, откуда 5R₅⁴-5R₅²+1=0 и 80r₅⁴-40r₅²+1=0.

Решение задачи 12. Тут мы приводим оригинальное решение Адзимы, с одним лишь замечанием: он проводил вычисления с точностью в 14 знаков, и математические программы показывают, что ошибок у него не было!

(1)
100.9 = 101.0/100.1 = 7.943285; 100.8 = 100.9/100.1 = 6.309578;
100.7 = 100.8/100.1 = 5.011878; 100.6 = 100.7/100.1 = 3.981078;
100.5 = 100.6/100.1 = 3.162284; 100.4 = 100.5/100.1 = 2.511892;
100.3 = 100.4/100.1 = 1.995267; 100.2 = 100.3/100.1 = 1.584897.
(2)
100.09 = 100.10/100.01 = 1.230268; 100.08 = 100.09/100.01 = 1.202264;
100.07 = 100.08/100.01 = 1.174897; 100.06 = 100.07/100.01 = 1.148153;
100.05 = 100.06/100.01 = 1.122018; 100.04 = 100.05/100.01 = 1.096478;
100.03 = 100.04/100.01 = 1.071519; 100.02 = 100.03/100.01 = 1.047128.
(3)
102.56 = 102 × 100.5 × 100.06 = 100 × 3.162284 × 1.148152 = 363.0786.

Рис. 4.1. Ответ на табличку сангаку, вывешенную в 1879 году в храме Ага; 163x58 см. Содержит задачи, схожие с задачами 30-35 из этой главы.

Глава 4. Лёгкие задачи храмовой геометрии

Конфуций сказал: "Следует посвятить всё своё время обучению, забыв о еде и сне". Его слова ценны для нас. С детства я изучал математику и прочёл много книг по математике. Когда у меня возникали вопросы, я приходил к математику Оно Эйю: и спрашивал его. Я ценю уроки моего учителя. В благодарность к нему, я вывешиваю сангаку в этом храме. - Надпись на сангаку, вывешенной Сайто: Кунинори в 1828 году в храме Китамуки Каннон.

Задачи храмовой геометрии находятся не только в храмах. В эпоху Эдо 12 сборников задач сангаку было издано в печати, и сотни других задач остались в неопубликованных рукописях. Более того, некоторые деятели, вывешивавшие сангаку, безжалостно убирали задачи из более ранних коллекций. Ни об этих табличках, ни о книгах не следует думать, как о текстах в современном смысле; они никоим образом не составляют связного изложения васан. На отдельной сангаку задача, доступная 12-летнему ребёнку, может соседствовать с задачей, которая поставит в тупик выпускника ВУЗа. Частично, причина этого в том, что сангаку часто создавались группами людей, возможно - целым классом в дзюку, учащиеся в котором, конечно же, имели разные уровни.

Подобное положение дел превращает отбор и представление задач сангаку в своего рода вызов. Мы предпочли упорядочить задачи более по возрастанию сложности, чем по источникам, и по возможности сгруппировать вместе схожие задачи. И ещё раз: эти примеры - не "набор задач", разработанный инструктором для математического воспитания, а в основном случайная выборка из работ приверженцев решения геометрических загадок, которые их радовали.

В главах 4-6 мы предлагаем подборку из примерно 90 задач сангаку, выстроенных от тривиальных до практически невозможных. Большинство задач данной главы, посвящённой примерам попроще, взяты прямо с табличек (конкретнее, с первой выставки сангаку, упомянутой в предисловии), и некоторые из них можно увидеть в цветном разделе книги. Остальные задачи взяты из только что упомянутых коллекций и рукописей. Из опубликованных коллекций сангаку первая и, наверное, самая знаменитая, принадлежит Фудзите Кагэну. Книга Фудзиты Синпэки санпо: ("Священная математика") появилась в 1789 году и содержит задачи из 26 табличек, вывешенных между 1767 и 1789 годами. Во 2-м издании, 1796 года, Фудзита добавил задачи с ещё 22 табличек, вывешенных с 1790 по 1796 годы. Святилища, в которых эти таблички находились, были разбросаны по обширной области Японии, и в результате имя Фудзиты распространилось на столь же обширную область. В продолжении 1807 года Фудзита записал содержимое 50 табличек, вывешенных с 1796 по 1806 годы. Из 48 задач первой книги были уничтожены или потеряны все кроме одной, из храма Сакурай в префектуре Аити. Из 50 табличек второй части выжила тоже лишь одна, висящая в святидище Исаниха в префектуре Эхимэ.

Рис. 4.2. Ещё одна печать на дощечке из Дзинко:-ки (на сей раз издание 1788 г.)

Касательно остальных коллекций, хотя одна такая книга и появилась в 1873 году, после падения сёгуната, все задачи в ней датируются началом эпохи Эдо, до того, как влияние Запада стало ощутимым. Мы, также, цитируем много задач из неопубликованных рукописей. Для каждой задачи и для каждого решения мы указываем автора (если его имя дошло до нас) и источник, будь то табличка, книга или рукопись. Все эти книги печатались, в духе Гэнроку, на рисовой бумаге с помощью деревянных матриц, и сами являются произведениями искусства. Большинство их весьма редки, а приводимых нами решения, по большей части, ранее ни разу не появлялись на Западе.

Первые 3 примера данной главы, на самом деле, являются не геометрическими, а так называемыми диофантовыми - алгебраическими задачами, требующими целочисленных решений. 1 По типу они в духе некоторых китайских задач из главы 2. Практически все остальные задачи относятся к геометрии плоскости, хотя некоторые из последних требуют дополнительных простых вычислений. Мы верим, что большинство из них будет доступно учащимся высшей школы.

1. См. Conrad Totman, Early Modern Japan, стр.186 ("Для дальнейшего чтения", глава 1, стр.338)


2. Ёрё: - имя собственное, и дословно значит "почитание престарелых"


3. Ныне - префектура Сидзуока


4. На Западе он обычно упоминается, как Камбэй Мо:ри


5. Настоящее название этой брошюры неизвестно, поскольку её титульный лист утерян.

6. Точнее, Архимед поучил двустороннюю оценку π, помещая окружность между двумя правильными многоугольниками и зная, что длина окружности больше периметра вписанного многоугольника и меньше описанного. С помощью правильного 96-угольника он получил оценку 3 10/71 < π < 3 1/7.

7. На Западе обычно известен, как Кова Сэки.

8. Сёгунат Токугава ограничил владение каждого местного феодала одним замком, и в результате в бедную сражениями эпоху Эдо бывшие ранее сильными военными крепостями "города-замки" стали административными центрами. Математик Ямагути Кандзан часто говорит о них в своём дневнике (гл.7).

9. Охиси Манабу, http://library.u-gakugei.ac.jp (на японском).

10. Конечно, если Гуттенберг вообще использовал наборный шрифт: см. Tony Rothman, Everything's Relative and Other Fables from Science and Technology (Wiley, Hoboken, N.J., 2003).

11. Иногда известен под именем Тёкуэн Адзима.


12. Smith and Mikami, стр.273 ("Для дальнейшего чтения, глава 1").

1. См. "Для дальнейшего чтения" к этой главе; Ronan, Science and Civilization, гл.1; Cullen, Astronomy and Mathematics, гл.3 ("Для дальнейшего чтения, гл.2")


2. см. Li Di, Chinese Mathematics, а также Martzloff, Chinese Mathematics, стр.215. В качестве вероятной даты он указывает 1377 год. ("Для дальнейшего чтения, гл.2")


3. Martzloff, Chinese Mathematics, стр.160 ("Для дальнейшего чтения, гл.2"). Можно, также, отметить, что и на Западе, до распространения уравнений, было привычным учить формулы или алгоритмы, запоминая их в стихотворной форме.



4. Длины: 1 сун = 2.3 см., 1 сяку = 10 сун = 23 см. 1 бу = 5 сяку = 1.15 м. 1 дзё: = 2 бу = 2.3 м. 1 ри = 360 бу = 414 м. Площади: 1 бу = 32 м2

   Объёмы: 1 сё: = 0.2 л. 1 то = 10 сё: = 2 л. 1 коку = 10 то = 20 л. Веса: 1 сё: = 0.58 гр. 1 рё: = 24 сё: = 13.9 гр. 1 кин = 16 рё: = 222.4 гр. 1 коку = 120 кин = 26.688 кг.

   В этой главе мы, в основном, используем оригинальные единицы измерения, например - бу вместо метра. Замена единиц измерения на современные сделала бы числа в задачах весьма смущающими. Однако если читатель пожелает перейти от традиционных единиц измерения в Китае II в. до н.э. - II в. н.э. к современным, он может это сделать с помощью следующей таблицы.


5. Отметим, что традиционно единица измерения бу использовалась как для длины, так и для площади. Мы же будем говорить о "квадратных бу", и аналогично - для других единиц измерения.


6. Кин - традиционная единица измерения как для денег, так и для веса (см. пред. прим.), хотя в терминах современных валют её значение и неизвестно. В старом Китае 1 кин равнялся 16 рё:, 1 рё равнялся 24 сё:, и ответ к данной задаче, равный 6/5 кин, имел вид "1 кин, 3 рё: и 4 + 4/5 сСэйё: санпо:ё:", поскольку 6/5 = 1 + 3/16 + (1/16)*(1/24)*(4+4/5).


7. Хики - ещё одна традиционная единица длины, использовавшаяся для измерения ткани; 1 хики = 4.7 м.


8. Oyestein Ore, Number Theory and its History (Dover New York, 1976), стр.118.


9. см. Martzloff, Chinese Mathematics, стр.310 ("Для дальнейшего чтения, гл.2")


10. См. Ronan, Science and Civilization ("Для дальнейшего чтения", гл.2)


11. См. http://www-groups.dcs.st-and.ac.uk/history/Mathematicians/Horner.html, а также Cooke, History of Mathematics, стр. 415 ("Для дальнейшего чтения", гл.2).


12. см. http://www-groups.dcs.st-and.ac.uk/history/Mathematicians/Al-Karaji.html


13. Сколько 1 мон стоил в древнем Китае, мы не знаем, но в Японии XVII века он стоил около четверти доллара.


14. В 1592 г. значение коку было равно 71.616 кг. (риса), поэтому речь в задаче идёт о 16139 кг. в целом.


15. Как и для мон, денежный эквивалент для рё и бу (из следующей задачи)
в Китае XVI века неизвестен. Авторы верят, что они примерно равны 30 долларам и 3 долларам соответственно.

1. 1 кэн = 1.8 м. 1 квадратный кэн = 1 кэн x 1 кэн = 1 цубо.


2. Тан - единица измерения длины для отрезов ткани шириной около 34 см. 1 тан такой материи - это примерно 10 м.


3. 1 сё: = 1.8 литра. Японское сё: отличается от китайского сё:.


4. См. Coxeter & Grietzer, Geometry Revisited. Там, также, приводится другое решение.


5. Иногда - Имамура Чисё.


6. Иногда - Такэбэ или Такэбэ Кэнко.


7. "Стать самураем" в основном значило получить от клана назначение на какую-либо официальную должность.


8. Иногда говорят, возможно основываясь на этой задаче, что Адзима построил таблицу логарифмов; однако в его книге доказательств этому мы не нашли.


9. Если (p,q) взаимно просты, то и (p,r), и (q,r) взаимно просты.


10. На Западе, иногда - Айда Аммэй

1. По имени Диофанта из Александрии (ок. 200-284 гг. н.э.), которого иногда называют "отцом алгебры".

1. Зачастую ками ошибочно переводится на русский (и почти всегда на английский, как и в оригинале данной книги) как "боги" (gods), что сильно искажает контекст. Впрочем, перевод "духи" тоже недостаточно точен (м.б., в христианском контексте точнее "ангелы-хранители").

2. Как видно по основной коллекции изображений сангаку в Сети, сайту доктора наук Хироси Котэра wasan.jp, оригинал этой "таблички 1683 года" уничтожен пожаром 1975 года, и нынче есть лишь реконструкция 1983 г. Тут на ум приходит и то, что другая "древнейшая из сохранившихся сангаку", тоже датируемая 1683 г., тоже представлена лишь реконструкцией (1975 г.), и то, что "первое ознакомление Запада с сангаку" произошло лишь после этих реконструкций.
   
   Вот сводный результат хронологического упорядочения содержимого wasan.jp (этот источник содерит изображения ≈360 деревянных артефактов - около 40% от числа доживших до наших дней, т.е. данная выборка с избытком является статистически значимой):

   1683-1701: 6 артефактов (3 без чертежей, 1 санги, 2 реконструкции 1975 и 1983 г.)
   1739-1771: 4 (2 реконструкции, 1 с ошибочной датировкой, 1 бумажный черновик)
   1779-1790: 10
   1791-1800: 14
   -------------
   XVII в. -  5 артефактов (ни одной оригинальной сангаку не сохранилось),
   XVIII в.- 29 артефактов, 
   XIX в. - 276 артефактов,
   XX в.  -  46 артефактов,
   XXI в. - 6 артефактов.
   (см., также, детальный список)
   

   Итог: древнейшие сохранившиеся оригинальные сангаку датируются 1780-ми годами.

   Кстати, с середины XX века в Японии выходит ежеквартальный журнал по истории васан, одним из авторов которого является Фукагава.

3. Дословно - "японский счёт". Иероглиф 算 [сан] имеет в различных словах значения "счёт", "вычисление", "число", "счёты", "вероятность". Слово же "математика", 数学 [су:гаку] выражается совсем другими иероглифами.

4. Интересное замечание сотрудника Принстонского университета, не понаслышке знакомого с положением дел в высшей школе США в 2008 году.

5. Формально, приводимое решение неверно, поскольку не учитывает остаток при делении на 2, а в силу отсутствия как доказательства, так и общей формулировки, данную задачу можно назвать лишь прототипом/истоком реальной "китайской теоремы об остатках".

6. Маленькая неточность. x = r (mod m) значит лишь, что x-r делится на m. Число r не обязано быть меньше m.

7. На самом деле, эта длина примерно равна 11-кратному расстоянию от Земли до Луны.

8. См., например, статью о числе π.

9. Не только "в васан"; этот метод даёт вообще все примитивные пифагоровы тройки. Общеизвестно, что условия (p=2mn, q=m²-n², r=m²+n²) являются не только достаточными, но и необходимыми.

10. То, что у квадрата радиус вписанной окружности равен половине стороны, а описанной - половине диагонали, конечно, очевидно и без синусов. Но тут автор, возможно, просто хочет привести серию многочленов для r_n и R_n для пытливого читателя.

По истории математики весьма полным и заслуживающим доверия является сайт MacTutor History of Mathematics Archive.
В нём нет специального раздела по японской математике, но зато есть биографии некоторых математиков, упоминающихся в данной книге.

На японском:

• Сайт по васан Фукагавы и Хорибэ
• Японский перевод статьи в Scientific American

Глава 2. Китайские корни японской математики

На английском:

• Yoshio Mikami, The Development of Mathematics In China and Japan (Chelsea New York, 1974; reprint of 1913 edition).
  
• David Smith and Yoshio Mikami, A History of Japanese Mathematics (Open Court, Chicago, 1914).
  
• Colin A. Ronan, The Shorter Science and Civilization in Ancient China: An Abridgement of Joseph Needham’s Original Text (Cambridge University Press, Cambridge, 1995), Vol. 2.
  
• Jean-Claude Martzloff, A History of Chinese Mathematics (Springer, Berlin, 1995).
  
• Christopher Cullen, Astronomy and Mathematics in Ancient China: The Zhou Bi Suan Jing (Cambridge University Press, Cambridge, 1996).
  
• Roger Cooke, The History of Mathematics: A Brief Course (Wily-Interscience, New York, 2005).

В сети:

На японском:

Глава 6. Ещё более сложные задачи храмовой геометрии

Глава 10. Введение в инверсию

• 朝日新聞 (Асахи Симбун) - одна из крупнейших японских газет


• 織田信長 (Ода Нобунага, 1534-1582) - сёгун эпохи смуты, начавший объединение Японии


• 関ヶ原 (Сэкигахара) - место известной битвы 1600 г.


• 東大寺 (То:дайдзи) - "Великий Восточный Храм" в городе Нара


• 豊臣秀吉 (Тоётоми Хидэёси, 1537-1598) - крупный даймё, предшественник Токугавы Иэясу


• 徳川家康 (Токугава Иэясу, 1543-1616) - сёгун (1603-1605)


• 深川英俊 (Фукагава Хидэтоси) - японский математик конца XX в., первым указаший Западу на васан


• 会田安明 (Айда Ясуаки, 1747-1817) - основатель "Наилучшей математической школы"


• 九章算術 - "9 глав искусства счёта" (китайский классический учебник)