Как применять санги

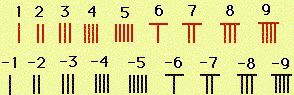
Для вычислений в эпоху Эдо в Японии использовались счётные палочки санги (算木).

Обычно красные санги обозначали положительные числа, а чёрные - отрицательные.

Чтобы решить кубическое уравнение -9 + 3x + 2x² + x³ = 0, расположим санги так, как показано на fig 1.

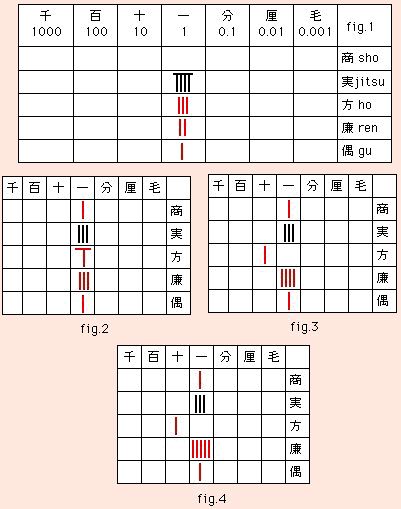Верхний ряд (sho) предназначен для санги, представляющих корень,

второй ряд (jitsu) - для коэффициента при нулевой степени x,
третий (ho) - для коэффициента при x,
четвёртый (ren) - для коэффициента при x²,
пятый (gu) - для коэффициента при x³, и т.д.

Положив 1 в sho, строим fig.2:

sho1*gu1 + ren2 = 3 (новое ren)
sho1*ren3 + ho3 = 6 (новое ho)
sho1*ho6 + jistu(-9) = (-3) (новое jitsu)

Положив на fig.2 единицу в sho, строим fig.3:

sho1*gu1 + ren3 = 4 (новое ren)
sho1*ren4 + ho6 = 10 (новое ho)

Аналогично fig.3, строим fig.4:

sho1*gu1 + ren4 = 5 (новое ren)

Вышеуказанные операции означают, что мы получили [уравнение]

подстановка в которое x = y + 1 даёт

Эти преобразования аналогичны символьной схеме Горнера:

fig.1 　1)　-9　　3　　2　　1
　　　　 　　　6　　3　　1
　　　　　   ----------------
fig.2　　　　-3　　6　　3　　1
  　　　　　　　　　4　　1
　　　　　　　　  ------------
fig.3　　　　 　　10　  4　　1
　　　　　　 　　　　　　 1
　　　　　　　　　　   --------
　　　　　　　 　　　　　 5　　1

fig.4 　　 -3 + 10y + 5y^2 + y^3 = 0

Источник: wasan.jp (д-р Котэра Хироси [小寺　裕])

eng->rus: shogi.ru, Д.К., 28.9.11 (версия 24.11.11)